technique-math-2bac.svt
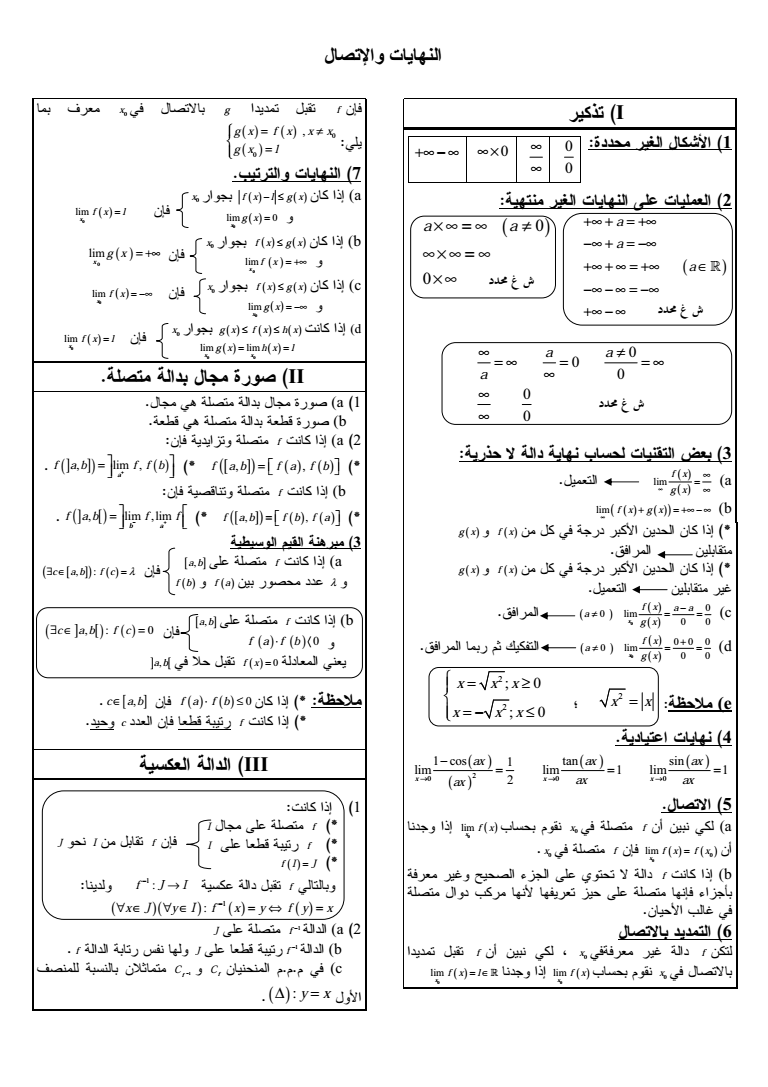
I a a a a a a a a a lim f x g x lim f x g x b g x f x g x f x c 0 limx 0 0 f x a a a g x d 0 0 0 0 limx 0 0 f x a g x quot quot e 2 x x 2 2 x x x x x x 2 0 0 0 1 cos tan sin 1 lim lim 1 lim 1 x 2 x x ax ax ax ax ax ax amp x0 f amp a limx amp f x limx x0 f f x f x -012 f amp b 3amp3quot03amp-4 f f amp 5 x 2 0 amp x limx amp f x limx f x l 2 g f 6 x g x f x x x g x l amp x0 f x l g x a lim 0 x g x x0 f x g x b limx f x x0 f x g x c limx g x x0 g x f x h x amp d 0 0 lim lim x x g x h x l ampII 78a 9798b f amp a lim f a b f a f b a f a b f f b amp f amp b lim lim f a b f b f a b a f a b f f amp a b 0 f amp a f b f a a b 0 f amp b f a f b a b f x 0 amp c a b f a f b 0 quot c 9 f amp III amp 1 I 0 f I 09 f f I J 0 f 1 f J I amp 1 x J y I f x y f y x a 1 f J 0 b 1 f f ltquotamp3 J 09 ampamp c Cf 1 f 6amp amp C y x limx f x l limx g x limx f x limx f x l c a b f c c a b f c 0 J amp I f
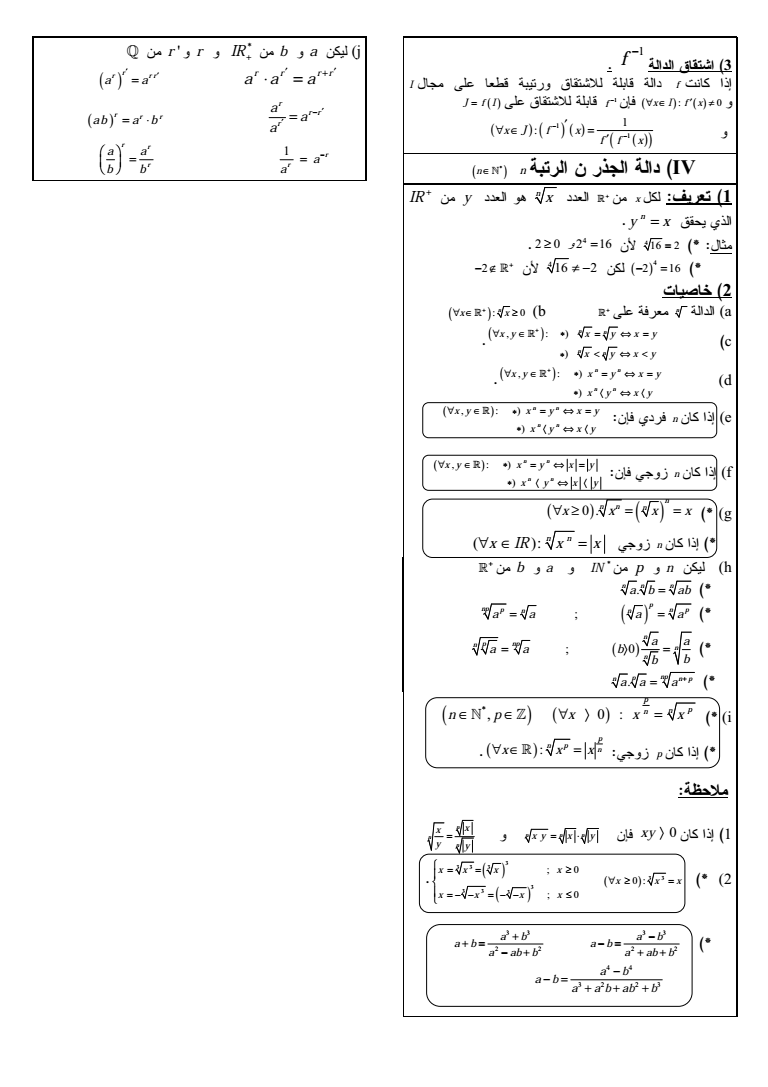
3 1 f I 0 9 f amp x I f x 0 1 f J f I 0 1 1 1 x J f x f f x n IV n x - n IR y 7 x 1 n y x 4 16 2 4 2 0 2 16 4 2 16 4 2 16 2 a 0 n 0 b n x x c n n n n x y x y x y x y x y lt lt d n n n n x y x y x y x y x y 1 n e n n n n x y x y x y x y x y n f n n n n x y x y x y x y x y g n n n n x x x x n n n x IR x x p n h b a IN n n n a b ab p np p n n n p a a a a n n p np n n a a a a b b b n p np n p a a a i p n n p n p x x x p p n p x x x n quot n x y x y n n xy n n n x x y y 2 3 3 x x x 0 3 3 3 3 3 3 3 3 x x x x x x x x 3 3 3 3 2 2 2 2 a b a b a b a b a ab b a ab b 4 4 3 2 2 3 a b a b a a b ab b b a j IR r r r r r r a a a r r r r a a r r r r a a a r r r a b a b 1 r r a a r r r a a b b

I I U U I n u n n n I U n I U M n M a n I U m n m quotb quot c M m n n I m u M n n I U k 0 n I U k n n n U n U U n n1 a n U U n n 1 amp b n U U n n1 amp c n U U n n 1 ampamp d n U U n n1 e p n u u p n Un 1 p n u u p n amp Un 2 Un 3 u u n n 1 Un u u n n 1 0 - amp Un u u n n 1 0 - amp Un u u n n 1 0 - ampamp Un u u n n 1 0 - Un u u n n 1 0 - II 1 n n U r n U U r n n 1 r Un a 01 21 u u n n 1 3 Un b 01 u u cte n n 1 43 1 0c a c b 2 2 a b b un 0 1 r 5 u0 n U U nr n 0 1 u1 10 1 1 U U n r n 1 u2 10 2 2 U U n r n U p n U 6 U U n p r n p r 5 58 pn 37 Un 1 r 5 u0 0 1 2 1 2 n n u u S u u u u n u0 S 9 un S 9 S 9 n 1 1 1 2 2 n n u u u u u n 0 1 0 1 1 2 n n u u u u u n 6 1 1 2 p n P p n u u u u u n p III 1 n n u q 1 1 n n n U qU q 1 8 1 7 a 01 21 lt Un1 3 1 Un b Un u q u n n 1 43 1 cba 0c 1 2 ac b

n u0 0 1 q 5 1 u n n n u u q 1 1 u1 10 n p u u q n 1 un p u 6 q 5 n p u u q n p 58 pn 37 Un 0 1 q 5 1 U0 1 q gt 1 0 1 0 1 1 n n q S U U U U q u0 S 9 S 9 n 1 S u u u n u 0 1 0 1 n q 1 0 1 1 0 1 1 1 n n q u u u u q q 1 2 1 1 1 n n q u u u u q 6 1 1 1 1 n p p p n p q u u u u q IV lim n q 0 1 1 1 1 lim 1 1 n q q q q q quot amp4 U l V n n V n U n a lim 0 lim V U l n n amp4U V n n V n U n b lim lim V U n n lim lim U V n n amp4V U W n n n W n V n U n c lim lim lim V W l U l n n n 5 5 Un 5 U Vn n 7U V n n V n U n a amp4 V n U n lim lim U V n n b quotamp c U f U n n 1 I f n n 1 U I U f U f I I - l 5 5 Un I f - f l l

I a1 2 2 z a ib a b 1 i ab z a ib z b i 2 i i 1 z quot z a ib c R z a o z amp a Im z b z amp b z a b 0 - z z ib a 0 b a b a a a a ib a ib b b a a ib b II ab z a ib - z a ib - z z a z z z z z z i b z z z z z z c 1 2 1 2 n n z z z z z z z z z z d 1 2 1 2 n n n n z z z z z z z z z z z z n e 1 1 z z z z z z z x iy f 2 2 2 2 Im z z x R z z z iy i z 2 2 zz x y III ab z a ib - z z 1 2 2 z zz a b quot z a z a a z b z ib b 2 2 2 z z z z zz a b z z z z z z 0 0 c d 1 2 1 2 n n zz z z z z z z z z n n z z e 1 1 z z z z z z 1 1 2 z zz zz z z z z 2 2 a ib a ib c id a ib c id c id c id c id c d amp IV 565 P 2quot34 1 2 o e e M z a ib P M x y a aff M u x y b v u 7 z a ib aff u z z M x y z a ib c M z P u x y 7 z a ib d z 2 u z v a 2 1 aff e i aff e aff o 1 0 b z M z x ox z M z ox z M z x o c z i M z y oy z i M z oy z i M z y o quot a aff M aff M M M aff MM aff M aff M MM aff M aff M b aff u aff v u v aff u v aff u aff v aff u aff u u aff u A B G c 1 aff G aff A aff B AB- I d 1 2 aff I aff A aff B 789C B A e c B A z z z C B A A B C A B A z z z z

- amp V 8z M z z 1 e OM arg z arg 2 z e OM 1 arg 0 2 arg 2 arg z z z z z z k arg 2 2 arg 2 2 arg 2 z i z z i z z i z k z lt arg 2 z z r z r i cos sin quot z r z i z re r r r r 2 a z a ib b 2 2 2 2 2 2 2 2 2 2 cos sin a b z a ib a b i a b a b a b i a b cos sin cos sin i i c cos sin cos sin i i cos sin cos sin i i sin cos cos sin 2 2 i i 1 1 n n r r rr r r n r r r r r r r r arg arg arg 2 arg arg 2 arg arg arg 2 1 arg arg 2 arg arg 2 n zz z z z n z z z z z z z z z i i i e e e n i in e e i i e e i i i e e e 1 i i e e 1 i e 2 i i e 2 i i e 1 arg 2 arg arg 2 e u aff u u v aff v aff u 1 arg 2 arg 2 B A D C B A e AB z z z z AB CD z z 1 C A B A z z z z 1 arg 0 2 C A C A B A B A C A B A AC z z z z AC AB AB z z z z z z AB AC z z Moivrequot cos sin cos sin n i n i n Euler quot 1 cos 2 1 sin 2 ix ix ix ix x e e x e e i 2cos 2 sin ix ix ix ix e e x e e i x 47 gt 1 2 1 i i z e z e 1 2 cos sin cos sin cos cos sin sin 2cos cos 2sin cos 2 2 2 2 2cos cos sin 2 2 2 i i z z e e i i i i i 1 2 cos cos sin sin 2sin sin 2cos sin 2 2 2 2 2sin cos sin 2 2 2 z z i i i A 2 2 2 1 2 2 2cos 2 i i i i i i z z e e e e e e 2 2 2 1 2 2 2 sin 2 i i i i i i z z e e e e e e i - 01 VI z z z n n z Z n a z a Z r A Z 2 01 1 n k k z r k n n n n A 2 1 k k w n k n 01 1

01 5 a Z r Z 2 2 Z r r 1 Z 2 u r u 1 b 02 1 Z a 1 2 Z a a u u a Z 02 2 Z a a 2 2 2 Z a i a i a u u i a Z 023 Z ib b 2 2 2 2 1 1 2 2 2 b b b Z ib i i i 1 Z 2 b u u i 02 4 Z ib b 2 2 2 2 1 1 2 2 2 b b b Z ib i i i 1 Z 2 b u u i b 0 0 a Z a ib 02 5 1 Z i 3 4 z x iy B 2 2 2 z x y ixy 2 2 2 2 Z 5 z x y 2 2 2 2 2 2 2 3 1 2 4 2 5 3 x y z Z z Z xy z Z x y quotECDC 2 x 1quot x 1 2 2 x quotE FC C 2 2 8 y 2 y 4 y 2 quot y 2 quot G47 y x xy 2 0 C9 1 2 x y quot 1 2 x y u u i 1 2 Z II1 4 VII quot 2 a 0 az bz c 0 B 2 b ac 4 1 9 0 H1 2 b z a u u 0 H 19 2 b u z a 2 b u z a 2 a 0 az bz c 0 2 1 1 z z 1 2 1 2 b z z a c z z a 2 a 0 az b z c 2 0 quot b ac 7 0 H b z a 1 97 0 H 1 2 b u z a 2 2 b u z a u
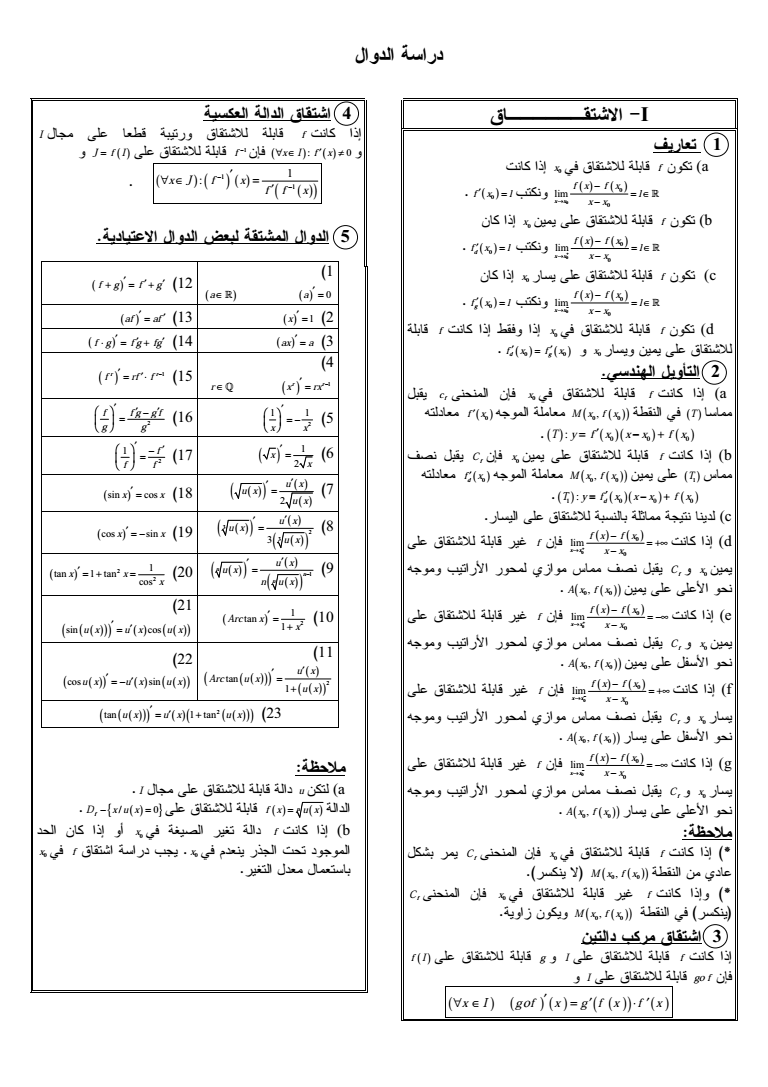
I quot f a 0 x limx x f x f x l x x f x l 0 f b 0 x lim x x f x f x l x x f x l d f c 0 x lim x x f x f x l x x f x l g f d 0 f x 0 x d g 0 0 f x f x quot cf x0 f a amp f x 0 M x f x 0 0 T T y f x x x f x 0 0 0 quot Cf x0 f b amp f x d M x f x 0 0 T1 T y f x x x f x 1 0 0 0 d amp c d lim x x f x f x x x f 0 x Cf -quot 0 0 A x f x e lim x x f x f x x x f 0 x Cf -quot quot 0 0 A x f x f lim x x f x f x x x f 0 x Cf -quot quot 0 0 A x f x g lim x x f x f x x x f 0 x Cf -quot 0 0 A x f x amp quot Cf x0 f 01 032 M x f x 0 0 -amp Cf x0 f 01 02 0 0 M x f x f I g I f I g f x I g f x g f x f x quot I quot f x I f x 0 1 f J f I 1 1 1 x J f x f f x quot amp I quot amp u a amp n D x u x f 0 f x u x amp 5 x0 4 4 amp f b 6amp amp 0 f amp x 0 x 4 quotampquot a a 0 f g f g af af 0 x 1 0 f g f g fg 0 ax a 0 r r 1 r x rx 0 r r 1 f rf f 2 1 1 x x 2 0 f f g g f g g 1 2 x x 2 1 f f f 2 u x u x u x sin cos x x 0 3 2 3 3 u x u x u x cos sin x x 0 1 n n n u x u x n u x 2 2 1 tan 1 tan cos x x x 2 1 tan 1 Arc x x sin cos u x u x u x 2 tan 1 u x Arc u x u x cos sin u x u x u x 0 2 tan 1 tan u x u x u x

I quot amp f 7 I amp f a x I f x 0 7 I f b x I f x 0 7 I f c x I f x 0 - f amp I quot amp f 0 8 946amp f amp x 0 x quot I quot amp f x I f x 0 amp Cf a x I f x 0 Cf b -quot - I quot amp f x I 0 0 f M x f x 8 946amp 0 x amp x0 8 9 4 3 6amp f a 0 0 lt M x f x quot amp 5 ampamp amp5 b gt amp f x II Cf quot x a 6 a 2a x D f Df xquot 017 2 01 f x D f a x f x Cf quot a b b 2a x D Df xquot 017 2 2 01 f x D f a x b f x 1 quot a quot gt 3 quot Cf limx a f x lim 5 x f x b lim 5 x f x 1 2 b lim 0 x a f x quot x a 6 a Cf lim 0 x f x b quot y a 6 Cf lim 0 x f x 6 limx f x x a limx f x x lt quot Cf b lim 0 x f x x quot lt quot Cf c lim 0 x f x a x lim 6 x f x ax lim f x ax b i quot y ax b 6 Cf lim f x ax ii lt quot Cf y ax amp quot y ax b 6 Cf lim 0 f x ax b y ax b 5ltquotA B ltquot f x ax b h x quot f x 5 lim 0 x h x amp quot Cf quot5 lt f x m amp quot a y m 6 Cf quot5lt f x 0 amp quot b quot Cg Cf quot5lt f x g x amp quot c 3 lt f x g x quot d gt Cg Cf 6 y ax b 6 Cf Campquot5e f x y 8 amp amp Cf f x y 0 01 amp Cf f x y 0 01

I o i j k v x y z u x y z 2 2 2 u x y z u v xx yy zz quot B x y z B B B A A A A x x z AB x x y y z z B A B A B A 2 2 2 AB x x y y z z B A B A B A quot n amp P amp amp P a P D amp P ax by cz d 0 b n a b c amp P amp quotamp c A 1 1 2 P amp amp n 21 1 amp amp M x y z P AM n 0 quot 1 2 1 1 0 2 1 2 1 1 2 0 x y z x y z P x y z 2 1 0 n 21 1 quot P amp P amp A P 1 1 2 2 1 0 x y z - P x y z 2 1 0 d 1 2 1 2 0 d quot d u a b c D D v a b c u v quot D D u v 0 aa bb cc 0 quot e u D i w v P quot D P u v u w u v u w u a b c D ii P n amp n u 1quot D P 0 a a b b c c u n 1quot D P 0 u n 0 2 P D iii P amp D amp amp D amp P ampamp f n Q P i n n n quot P Q 0 n n 0 n quot P Q 0 n P ax by cz d 0 ii Q a x b y c z d 0 aa bb cc 0 quot P Q quot g ampquot A P i P A quot H P A amp AH amp d A P AH P ax by cz d 0 ii ampquot 0 0 0 A x y z 0 0 0 2 2 2 ax by cz d d A P a b c II M quot amp 3 r - 34 amp M r 5 3r - a b c 34 S amp amp 2 2 2 2 x a y b z c r - amp - 2 2 2 x y z x y z 0 n P D n P A M n P u D n P D P H A
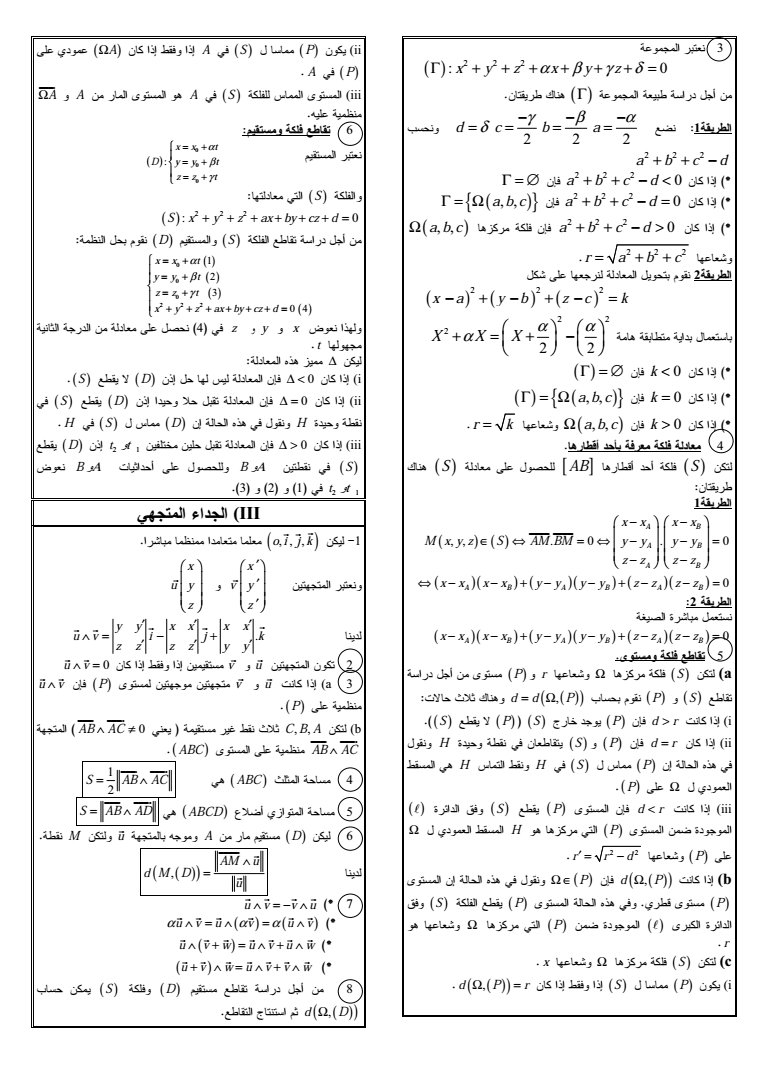
amp 2 2 2 0 x y z x y z quot63amp ampquotamp 7 quot 2 2 2 d c b a 2 2 2 a b c d 0 2 2 2 2 a b c d lt 0 0 2 2 2 a b c 2 a b c d 0 0 2 2 2 a b c 34 amp 2 a b c d gt 0 - 2 2 2 r a b c - amp quot 2 2 2 x a y b z c k amp3ampquot amp 2 2 2 2 2 X X X 2 k lt 0 0 a b c 2 k 0 0 r k -a b c 2 k gt 0 0 - 63 S amp 9 AB 3quot8 amp S quot quot 0 0 A B A B A B x x x x M x y z S AM BM y y y y z z z z x x x x y y y y z z z z A B A B A B 0 quot amp9 - 0 A B A B A B x x x x y y y y z z z z 0quot amp P r - 34amp S a 1lt63 d d P P S 7quot S 7quotltP S gt P 2 d r gt 1i H ampquotquot S P 2 d r ii quot 3 H B quot H S BP amp A3 P C 5 S 7quot P 2 d r lt 1 iii quot H 334 P -P 2 2 r r d amp A3 P 2 d P 1b 5 S amp 7quot P amp A3quot8 P 3 - 34 P C r x - 34amp S c d P r quotS P i A quot A S P ii A P A A 3 A S amp B iii amp quot 0quot x x t D y y t z z t S amp 2 2 2 S x y z ax by cz d 0 amp D S amp 7quot amp 2 2 2 1 2 3 0 4 x x t y y t z z t x y z ax by cz d amp amp amp 9z y x t amp A34 S 7quotltD B amp 2 lt 0 i S 7quot D amp 2 0 ii H S BD amp A3 H ampquot amp 2 gt 0 iii 2 1 7quotD t t B A 1 9 B A quot S 2 1 t t III o i j k D - x v y z x u y z y y x x x x u v i j k z z z z y y u v u v 0 quot u 1a v u v 2 P P amp AB AC 0 amp Equot C B A b amp AB AC ABC amp 3 ABC amp 1 2 S AB AC S AB AD 3 ABCD F4 amp u amp A D ampquot M AM u d M D u u v v u 0 u v u v u v 0 u v w u v u w 0 u v w u v v w 0 S amp D 7quot amp 7quot gt d D

I F 1 f IR x x Log ln F1 0 ln 0 IR a ln D 0 f x u x ln b f x D u x gt f x u x ln f x D u x ln1 0 c e 271828 ln 1 e ln r r Q e r ln r Q b gt 0 a gt 0 ln ln ln ab a b ln ln r a r a 1 ln ln a a ln ln ln a a b b ln ln a b a b ln ln a b a b lt lt ln ln ln ab a b ab gt 0 quot 0 quot a b ln ln ln gt a a b b 0 quot n ln ln a gt n a n a ln x 4 1 0 ln x x x gt ln u x u x u x ln u x u x u x quot5 lim ln x x a ln lim ln x x b ln0 c ln lim 0 x x x d lim ln 0 x x x e ln1 lim 1 x x x 1 ln lim 1 x 1 x x ln ln 0 ln ln 0 1 t v x t u x v x v x t t w x t v x a t II ln amp x x e a x x e x gt x e b 0 e 1 1 e e ln c x x e x ln 0 x gt x e x 0 d x gt x y e y ln y x r Q x y x y x y e e e x 1 x e e x x y y e e e rx x r e e x y e e x y x y e e x y lt lt x x x e e u x u x e u x e x ln x 0 1
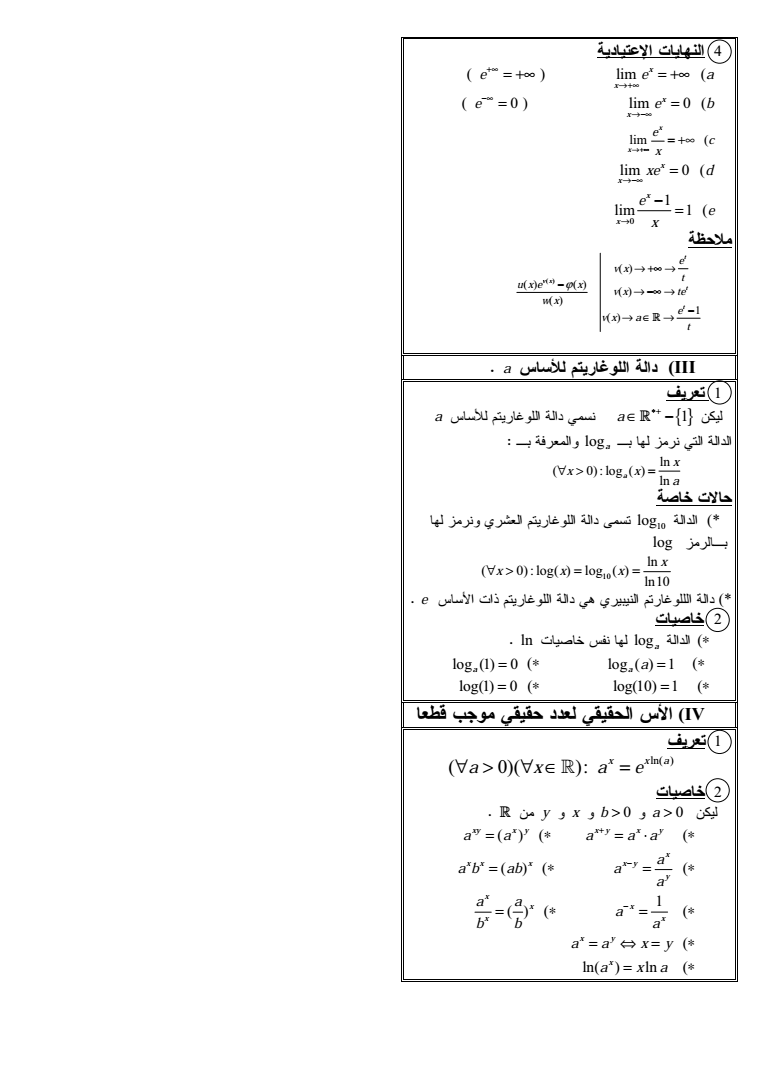
quot lim x x e a e lim 0 x x e b 0 e lim x x e c x lim 0 x x xe d 1 lim 1 x x e e x 1 t v x t t e v x t u x e x v x te w x e v x a t a amp III a 1 a amp log a ln 0 log ln a x x x a gt 10 log log 10 ln 0 log log ln10 x gt x x x e amp - log a ln amp log 1 a log 1 0 a a log1 0 log10 1 -- IV ln 0 x x a gt a x a e y x b gt 0 a gt 0 x y x y a a a xy x y a a x x y y a a a x x x a b ab x 1 x a a x x x a a b b x y a a x y ln ln x a x a
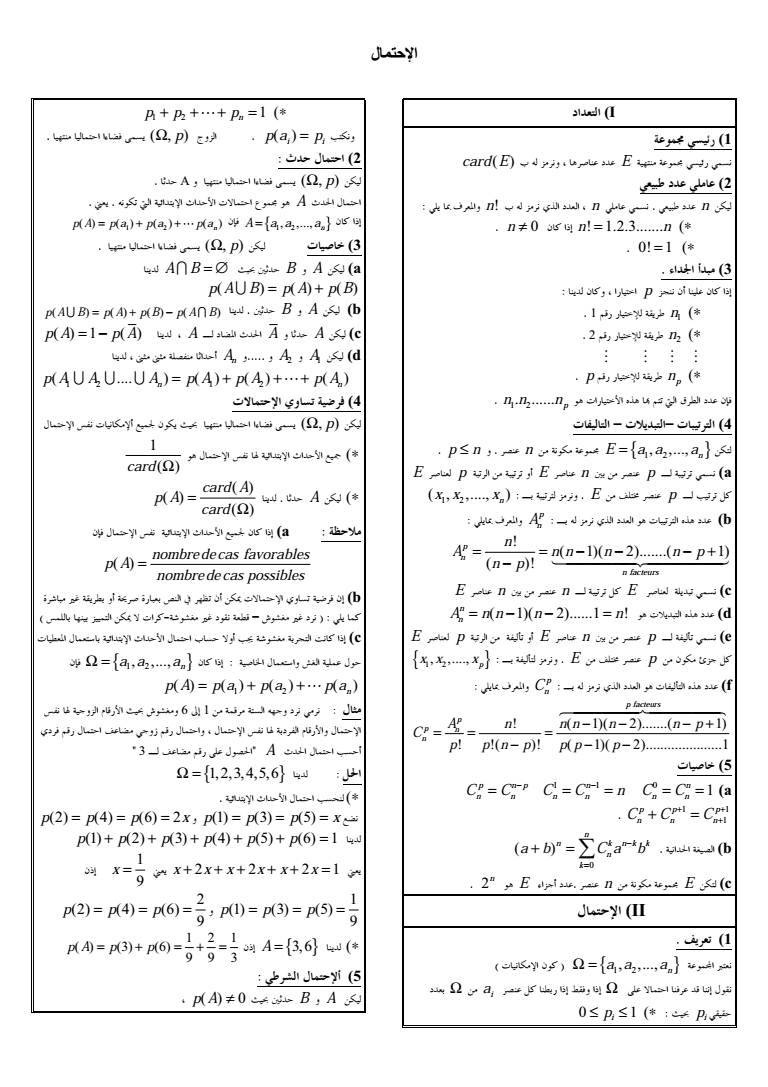
I 1 card E E 2 amp nampamp n quot n quot n 0 -amp n n 123 quot 0 1 3 -amp2amp p 01-amp 1 quot34256 n 2 quot 34256 n np quot p 34256 7amp28amp93ltampgtamp 1 2 n n np quot quot 4 1 2 E a a a n quot p n quotA n E p amp 1 E n CDA p B a BD quot E GHA p BEF- 1 2 n x x x BDampamp7 amp9 b p An amp 1 2 1 p n n facteurs n A n n n n p n p E n CDA n B F- E c 1 21 7I amp9d n A n n n n n E p ampJK1 E n CDA p BJK e BDJKquot E GHA p LMF- 1 2 p x x x BDampamp7JKamp9f p Cn amp 1 2 1 1 21 p facteurs p p n n A n n n n n p C p p n p p p p amp 5 a 0 1 n C C n n 1 1 n C C n n n p n p C C n n 1 1 1 p p p C C C n n n quot quotampNampOAampb n n k n k k n k a b C a b 2 E PampM1quotA n E c n quot II 1 QampR 1 2 n U 7Tamp-S a a a AF-gtDampZ6amp VW Xamp4Y6 i D a 66X i 0 1 p i p 1 2 1 n p p p E i i quot XampampPV p amp quot p a p 2 quot XA XampampPV p quot bquotltampampDTampampX8amp7W Xampa A NampY Xamp -amp 1 2 A a a a n 1 2 p A p a p a p a n quot XampampPV p amp 3 A B CX B A a p A B p A p B p A B p A p B p A B quotCX B A b p A p A 1 A BampNamp A X A c cdcdAJampX1 An quotquotquotquotquot A2 A1 d 1 2 1 2 n n p A A A p A p A p A 01 - 4 Y XTampeJ7T1f g XampampPV p Y XTampeJhampDTampampX8ampfi 1 card quotX A card A p A card Y XTampeJampDTampampX8ampf g-ampa 2quot nombre de cas favorables p A nombre de cas possibles kq rs6gtD1jk Dlampmn1o7W XTamp pb U e DD ampoW7amp-wquOrs6gt4vtuOrsS - 7gtampY xDampDTampampX8ampY Xamp XW1EyquOD0ampz-ampc -ampampY xampOamp YX 1 2 n a a a 1 2 n p A p a p a p a eJhMamp48amptuO 4 ampM 3 34Y XampG M34Y XampY XTampeJhDJamp48ampY XTamp BG34VYANamp A NampY XampE X1 123456 45 quot ampDTampampX8ampY XampE p p p x 2 4 6 2 p p p x 1 3 5 f p p p p p p 1 2 3 4 5 6 1 b x x x x x x 2 2 2 1 b 1 9 x 1 1 3 5 9 p p p 2 2 4 6 9 p p p A 36 1 2 1 3 6 9 9 3 p A p p 6 5 p A 0 CX B A
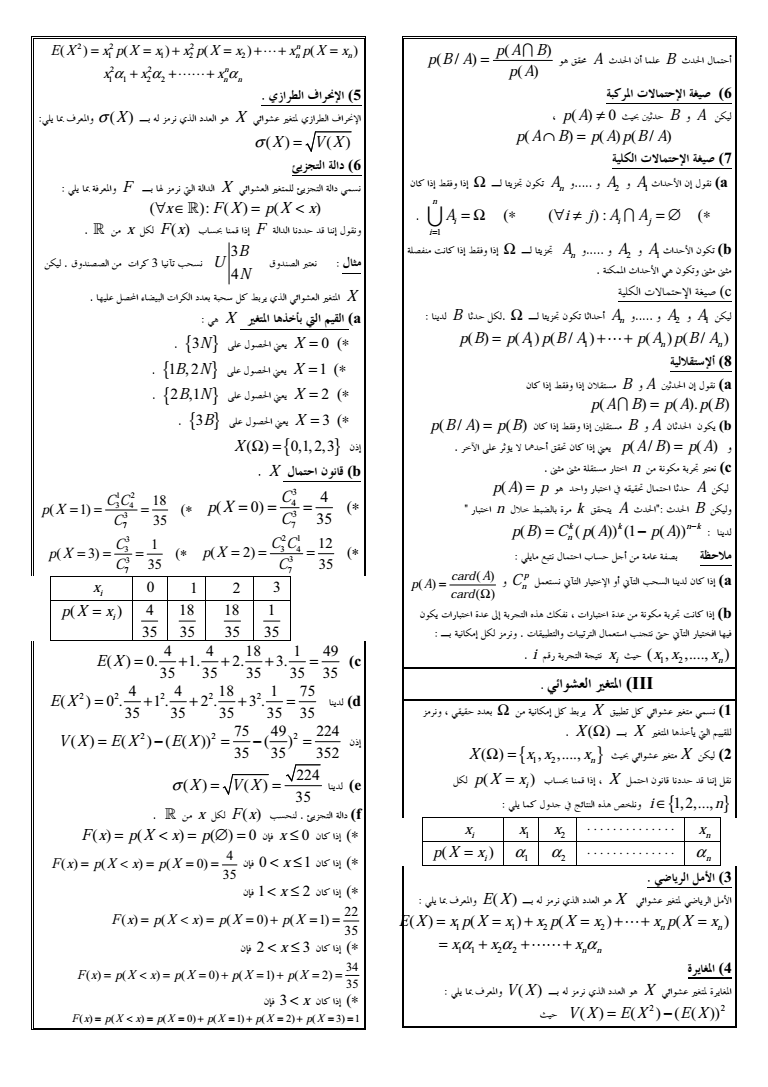
6 A Namp1 B NampY X1 p A B p B A p A 7 8 9 6 p A 0 CX B A p A B p A p B A 9 7 ampX8ampY6a A1 A2 quotquotquotquotquot An -ampZ6amp B i j i j A A 1 n i i A quot AJz-ampZ6amp B An quotquotquotquotquot A2 A1 ampX8ampb quot ampampX8amp cdcd amp7W XTampO c A1 A2 quotquotquotquotquot An B XFquot B ampX1 1 1 n n p B p A p B A p A p B A quot lt 8 -ampZ6ampI6 B A CNampY6a p A B p A p B p B A p B -ampZ6ampC6 B A Nampb quot 2ampVWX16-ampb p A B p A quot cdcd6 2amp n D Rc p A p Xamp 2ampm66Y XampX A 2amp n YI2Z Dk k 6 A NampNamp B 1 k k n k p B C p A p A n f Y Xamp XFM1JAD 2quot F amp2Tamp1ampE amp-ampa p Cn card A p A card 7amp 2ampkD0amp9J7amp 2ampkD z-ampb BDFquot76 gtamp7 ampY xampE0Xampamp 1 2 n X x x x i quoti 34D0amp0 x quot 6 9 8 III 66XD F-ZD X gtF- ampurO 1 quot X BD X rOamp2Kltamp36 ampurO X 2 1 2 X x x x n 4amp X F Xamp4X4F6 i F p X x -YMmamp9li n 12 n x 2 x 1 x i x n 1 2 i p X x 1 4gt 3 amp E X BDampamp X ampurO pampF8amp 1 1 2 2 1 1 2 2 n n n n E X x p X x x p X x x p X x x x x 98 4 ampV X BDampamp X ampurOkOamp 2 2 XV X E X E X 2 2 2 1 1 2 2 2 2 1 1 2 2 n n n n n n E X x p X x x p X x x p X x x x x A B C 5 amp X BDampamp X ampurOampgtampampTamp X V X DEF 6 amp F BDhltampampamp X ampuamprO 0ampamp lt x F X p X x quot x F F x 4amp F ampampX4Y6 AampR3 3 4 B U N quotAAamp7amp-E quot FAampP amp7ampampD xF-ZDamp ampuamprOamp X X 9 8 GHampIJ K a quot3N VYANampb X 0 quot1 2 B N VYANampb X 1 quot2 1 B N VYANampb X 2 quot3B VYANampb X 3 X 01 23 X LM b 3 4 3 7 4 35 C p X C 1 2 3 4 3 7 18 1 35 C C p X C 2 1 3 4 3 7 12 2 35 C C p X C 3 3 3 7 1 3 35 C p X C 0 1 2 3 i x 1 35 18 35 18 35 4 35 i p X x c 4 4 18 1 49 0 1 2 3 35 35 35 35 35 E X d 2 2 2 2 2 4 4 18 1 75 0 1 2 3 35 35 35 35 35 E X 2 2 2 75 49 224 35 35 352 V X E X E X e 224 35 X V X quot x F F x E quot0ampampf F x p X x p 0 lt x 0 -amp 0 1 lt x -amp 4 35 F x p X x p X lt 1 2 lt x -amp 22 0 1 35 F x p X x p X p X lt 2 3 lt x -amp 34 0 1 2 35 F x p X x p X p X p X lt 3 lt x -amp F x p X x p X p X p X p X 0 1 2 3 1 lt

I I b a I f quot b a f b a f x dx amp b a f x dx F b F a f quot F b b a a f x dx F x F b F a 01- 2 x - b b a a f x dx f t dt II I c b a I g f 0 1 a a f x dx 2 a b b a f x dx f x dx 3 b c b a a c f x dx f x dx f x dx 74563 4 b b b a a a f x g x dx f x dx g x dx 5 b b a a af x dx a f x dx a IR quot 6 x a F x f x dx f quot8 quot 9 a quotlt 0 x a b f x a b gt a7 b a f x dx 0 x a b f x a b gt b b a f x dx x a b f x g x a b gt c b b a a f x dx g x dx a b gt d b b a a f x dx f x dx quot a 8 1 b a f x dx b a f quotAB C b a Fb a E F c quotquotDb b a f x dx b a f c c 1 b a m f x dx M b a C G9 M m a b f quot C C quot GI Jb a 8H quot III amp 1 f FI KC4L5 g f ltquotI b a I g b b b a a a f x g x dx f x g x f x g x dx - 00IV f F 0 1 a 0 ax 1 r x r 1 1 1 r x r 1 r u u r 1 1 1 r u r 2 1 x 1 x u u 1 u 1 x 2 x u u 2 u 1 x ln x u u ln u x e x e ax e 1 ax e a f F u x u e u x e 2 1 1 x arctan x 2 1 u x u x arctan u x cos x sin x sin x cos x 2 2 1 tan 1 cos x x tan x cos ax b 1 sin ax b a sin ax b 1 cos ax b a 2 2 1 tan 1 cos ax b ax b 1 tan ax b a u x u x cos sin u x u x u x sin cos u x 2 u x u x 1 tan tan u x

1V 1 P x I dx ax b ax b P x 5 GU u u 2 2 1 I dx ax bx c C V quotF lt 0 gt a 2 p x ax bx c F 2 1 I dx u x t u x OP GU p x a x x P x gt 0 gt b Wlt 1 1 1 1 P x x x GU u u 0 gt c 2 2 1 1 x I dx dx x x x 3 2 P x I dx ax bx c P x 5 2 GUax bx c u u 2 1 u u 4 n I P x ax bdx n P x I dx ax b OP n t ax b I P x ax dx cos 5 I P x ax dx sin kx I P x e dx OPX D8 cos f x P x g x ax I P x x dx cos ln 6 I P x Arc xdx tan OPX D8 ln arctan f x x ou g x P x cos 7 kx I e ax dx sin kx I e ax dx I A I quot X D8 8 1 x I dx ae b x x x x x e e u I dx dx e ae b a be u 9 ln r x I dx x 1 ln 1 ln ln ln 1 r x r r I dx x x dx x x r 10 n u x v x I dx w x OPX D8 n w x f x w x g x quot 23V quot quot 1 F E a b lt a b f a E F Cf x b x a x Ox AE 9 E F b a f x dx u a 54 EF KquotDCf ltf 0 Ygt AE 8 b a f x dx u a EF YFquotDCf ltf 0 Ygt AE 8 b a f x dx u a 6Z E4 -Ygt AE b a f x dx f x dx E a b lt a b g f b E F F Cf Cg x b x a AE 9 E F b a f x g x dx u a 5 Cg KquotDCf ltf g Ygt AE b a f x g x dx Cg YFquotDCf ltf g Ygt AE b a g x f x dx -Cg NltCf Ogt AE b a g x f x dx f x g x dx i cm gt c j cm 9 N5quot 2 u a cm 8967 quot 2 7V 3 S a E F a GV z b z a S quot Ygt S a b IR t S t V a b b a S t dx u v 7z t c S ObCa 9S t 3 a b f b E Cf E 8 EF R E G quot gt 9G 9G 2 b a V f x dx u v
oussama
أرسلت .
- الملفات : الملفات.
- المستوى : الثانية باكالوريا.
- الشعبة : علوم الحياة والأرض.
- المادة : الرياضيات.
كلمات مفتاحية :
technique math 2bac svt
technique math 2bac svt