جميع دروس الرياضيات للجدع المشترك علمي

مجموعة الأعداد الصحیحة الطبیعیة مبادئ في الحسابیات تعاریف و خاصیات 1 - الأعداد الصحیحة الطبیعیة الزوجیة n - n زوجي یكافئ n یقبل القسمة على 2 n k 2 بحیث k یوجد یكافئ 2 n - الأعداد الصحیحة الطبیعیة الفردیة - n فردي یكافئ n لا یقبل القسمة على 2 n k 2 1 بحیث k یوجد یكافئ نتائج - مجموع عددین زوجیین ھو عدد زوجي - مجموع عددین فردیین ھو عدد زوجي - مجموع عدد زوجي و عدد فردي ھو عدد فردي - مربع عدد زوجي ھو عدد زوجي - مربع عدد فردي ھو عدد فردي 3- مضاعفات و قواسم عدد صحیح طبیعي kdm أعداد صحیحة طبیعیة d ل مضاعف m یكافئ m dk یكافئ d قاسم ل m 4- الأعداد الأولیة یكون العدد الصحیح الطبیعي أولبا إذا كان لھ قاسمان فقط مثال 0 لیس أولبا لأن لھ أكثر من قاسمان 1 لیس أولبا لأن لھ قاسم واحد أولیة أعداد 191713117532 5- القاسم المشترك الأكبر المضاعف المشترك الأصغر - القاسم المشترك الأكبر b a القاسم المشترك الأكبر ل a و b ھو جداء الأعداد الأولیة المشتركة بین تفكیكي a و b مرفوعة إلى أصغر أس نرمز إلیھ ب a b أو D ab المضاعف المشترك الأصغر المضاعف المشترك الأصغر ل a و b ھو جداء الأعداد الأولیة المشتركة و الغیر المشتركة بین تفكیكي a و b مرفوعة إلى أكبرر أس نرمز إلیھ ب a b أو M ab الحساب المتجھي I المتجھات جمیع متجھات المستوى تكون مجموعة تسمى مجموعة متجھات المستوى نرمز إلیھ ب v 1- تساوي متجھتین DC BA أربع نقط من المستوى P C DA B AB CD الأضلاع متوازي ABDC یكافئ لھما نفس الإتجاه نفس و CD یكافئ AB المنحى ونفس المعیار خاصیة من v و A من P توجد نقطة وحیدة B مھما تكن u u AB بحیث v من نتائج AC BC C D یكافئ AB 0 A B یكافئ 2- مجموع متجھتین علاقة شال AB BC AC نتیجة AB BA 3- ضرب متجھة في عدد حقیقي u v كان إذا k و متجھة فإن - ku لھما نفس الإتجاه و u - ku ku k u - مثال ملاحظة لھما نفس المنحى و ku إذا كان k gt 0 فإن u لھما منحیان متعاكسان و ku إذا كان k gt 0 فإن u 1

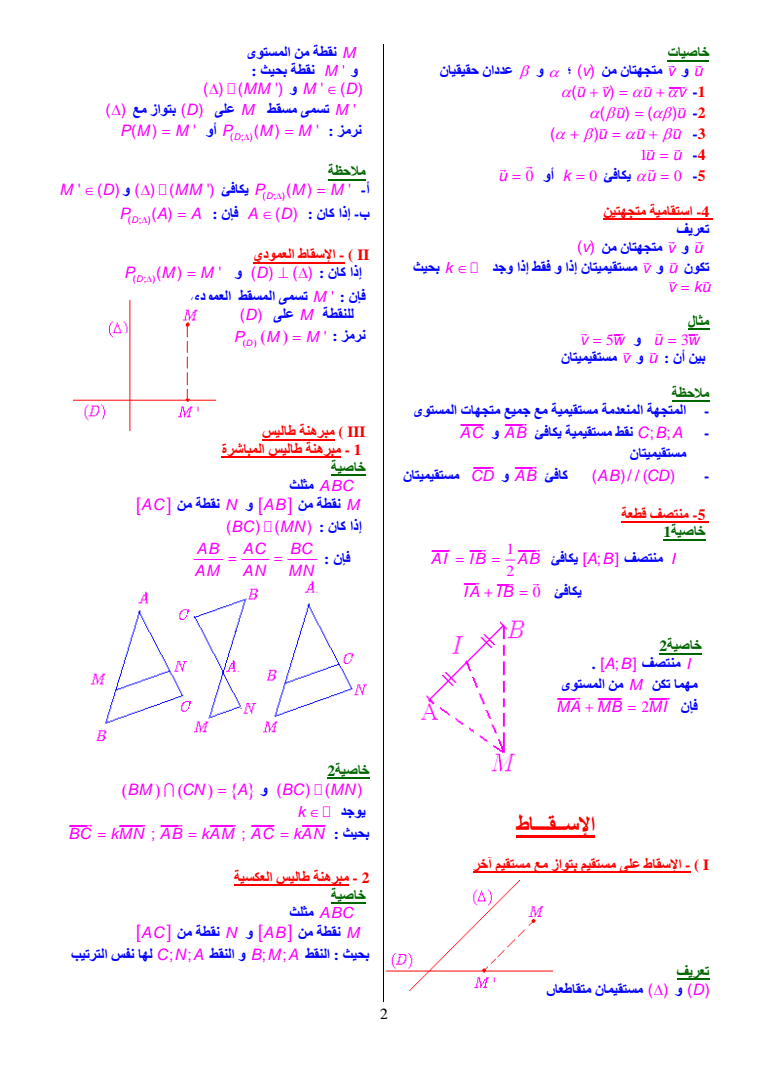
خاصیات u v و متجھتان من v و عددان حقیقیان uv u v -1 u u -2 uuu -3 1u u -4 u 0 -5 u 0 أو k 0 یكافئ 4- استقامیة متجھتین تعریف u v و متجھتان من v u تكون v و مستقیمیتان إذا و فقط إذا وجد k بحیث v ku مثال u w 3 v w 5 و و v بین أن u مستقیمیتان ملاحظة - المتجھة المنعدمة مستقیمیة مع جمیع متجھات المستوى AB یكافئ مستقیمیة نقط CBA - AC و مستقیمیتان AB كافئ AB CD - CD و مستقیمیتان 5- منتصف قطعة خاصیة1 یكافئ A B منتصف I 1 2 AI IB AB IA IB 0 یكافئ خاصیة2 A B منتصف I مھما تكن M من المستوى MA MB MI 2 فإن الإسقاط I - الإسقاط على مستقیم بتواز مع مستقیم آخر تعریف D و مستقیمان متقاطعان M نقطة من المستوى و M نقطة بحیث MM و M D M تسمى مسقط M على D بتواز مع نرمز PM M أو PMM D ملاحظة -أ M D و MM یكافئ PMM D P AA D فإن A D كان إذا -ب II - الإسقاط العمودي PMM D إذا كان D و فإن M تسمى المسقط العمودي للنقطة M على D نرمز PM M D III مبرھنة طالیس 1 - مبرھنة طالیس المباشرة خاصیة ABC مثلث M نقطة من AB و N نقطة من AC BC MN كان إذا فإن AB AC BC AM AN MN خاصیة2 BM CN A و BC MN k یوجد BC kMN AB kAM AC kAN بحیث 2 - مبرھنة طالیس العكسیة خاصیة ABC مثلث M نقطة من AB و N نقطة من AC بحیث النقط BMA و النقط CNA لھا نفس الترتیب 2

AB AC إذا كان AM AN BC MN فإن 3 - مبرھنة طالیس المباشرة بالإسقاط خاصیة نعتبر P P D L مستقیم ضمن المستوى لا یوازي A و B نقطتان مختلفتان من L إذا كانت C نقطة من L بحیث PC C و PB B و PA A فإن AC A C AB A B 4- معامل استقامیة متجھتین نعتبر P P D خاصیة AB kEF كان إذا PB B PA A و PF F PE E A B kE F فإن ID المجموعات 1- المجموعات - ھي مجموعة الأعداد الصحیحة الطبیعیة 123 - ھي مجموعة الأعداد الصحیحة الطبیعیة النسبیة 3 2 10123 - ID ھي مجموعة الأعداد العشریة النسبیة 10p a ID a p مثال 15 15 ID ID - ھي مجموعة الأعداد الجذریة a a b b مثال 2 2 ID 3 3 نتیجة ID - ھي مجموعة الأعداد الجذریة و الاجذریة تسمى مجموعة الأعداد الحقیقیة مثال 2 2 9 9 نتیجة ID 2- النشر و التعمیل خاصیة a b c ab ac a b c d ac ad bc bd المتطابقات الھامة -أ 22 2 2 a b a ab b 22 2 2 a b a ab b 2 2 abab a b -ب 33 2 23 3 3 a b a a b ab b 33 2 23 3 3 a b a a b ab b 3 3 2 2 a b a b a ab b 3 3 2 2 a b a b a ab b الترتیب في 1- الترتیب في تعریف b و a a b 0 یعني a b یعني a b 3

خاصیات quot الترتیب quot dcba أعداد حقیقیة أ إذا كان a b فإن acbc ب- إذا كان a b و c d فإن acbd ac bc فإن c 0 و a b كان إذا - ج ac bc فإن c 0 و a b كان إذا -د b 0 و a 0 و a b كان إذا - ھ فإن 2 2 a b و a b و- إذا كان a و b غیر منعدمین و لھما نفس الإشارة فإن 1 1 a b 2- التأطیر تعریف axb lt lt axb lt axb lt axb یسمى تاطیرا للعدد x سعتھ b a خاصیات y xdcba أعداد حقیقیة - إذا كان axb و cyd فإن ac x y bd - إذا كان 0 axb و 0 cyd فإن ac xy bd 111 - إذا كان 0 lt axb فإن axb 3- التقریب بإفراط وتفریط تعریف xba أعداد حقیقیة إذا كان axb أو gt axb أو gt axb أو axb lt lt فإن a یسمى تقریبا ل x بتفریط بالدقة b a b یسمى تقریبا ل x بإفراط بالدقة b a مثال 22 3143 3144 7 lt lt ل تقریب 3143 22 7 001 بالدقة بتفریط ل تقریب 3144 22 7 001 بالدقة بإفراط 4- المجالات تعریف a b بحیث حقیقیان عددانb a ab x a x b 2 a b a b المجال مركز ھو a b المجال سعة ھي b a ملاحظة axb یكافئ x ab 5- القیمة المطلقة تعریف x x OA القیمة المطلقة ل x خاصیات x -أ x x x x x r و x -ب x r أو x r یعني x r r و x -ج rxr یكافئ x r x rr یكافئ x r و x r یكافئ x r -د x rr یكافئ r و x -ھ a و ar xar یكافئ xa r x a ra r یكافئ نقول أن a قیمة مقربة ل x بالدقة r بنفس الطریقة gt xa r ملاحظة إذا كان axar فإن a قیمة مقربة ل x بتفریط بالدقة r إذا كان ar xa فإن a قیمة مقربة ل x بإفراط بالدقة r المستقیم في المستوى المستقیم في المستوى I المستقیم في المستوى Oi j معلم 1- تعریف A نقطة من المستوى u متجھة غیر منعدمة AM tu بحیث M النقط مجموعة ھو المستقیم D المار من A و الموجھ ب u 4

نرمز لھ ب D Au ملاحظة كل مستقیم معرف بنقطة یمر منھا و متجھة مو جھة لھ 2- التمثیل البارامیتري لمستقیم تعریف 0 0 المستوى من نقطة Ax y u منعدمة غیر متجھة 0 النظمة xx t t yy t تسمى تمثیلا بارامیتریا للمستقیم D المار من A و الموجھ ب u ملاحظة كل مستقیم یقبل عددا لا منتھیا من التمثیلا ت البارامیتریة 3- معادلة دیكارتیة لمستقیم أ- استقامیة متجھتین uab نعتبر v و det a uv a b b u المتجھتین محددة تسمى v و i j للأساس بالسبة خاصیة u v و det 0 u v یكافئ مستقیمیتان ب- معادلة دیكارتیة لمستقیم كل مستقیم D لھ معادلة دیكارتیة على الشكل 00 a b D ax by c 0 ملاحظة u ba - 1 D ل موجھة D - 2 مستقیم یمر من النقطة Amn D یوازي محور الأفاصیل یكافئ Dyn D یوازي محور الأراتیب یكافئ Dxm uab - 3 D ل موجھة b 0 یكافئ OI D a 0 یكافئ OJ D 4- كل مستقیم D لا یوازي محور الأراتیب لھ معادلة D y mx p الشكل على دیكارتیة و تسمى المعادلة الختصرة المختزلة للمستقیم D - m المعامل الموجھ ل D - p الأرتوب عند الأصل u m 1 D ل موجھة متجھة ملخص AM u و مستقیمیتان معادلة دیكارتیة معادلة بارامتریة det 0 AM tu AM tu II الأوضاع النسبیة لمستقیمین خاصیة1 u ب موجھ D u ب موجھ D و det 0 u u یكافئ D D det 0 u u یكافئ D یقطع D خاصیة2 D y mx p و D y mx p m m یكافئ D D m m یكافئ D یقطع D الحدودیات 1- حدودیة من الدرجة n تعریف و من x لیكن 1 10 n n a a aa أعداد 0 an حقیقیة 1 1 1 0 n n n n p x a x a x ax a p x أو p تسمى حدودیة من الدرجة n deg p n نرمز i na یسمى معامل الحد من الدرجة 0 i i 1 10 n n a a aa p الحدودیة معاملات مثال 5 2 px x x x 4 3 2 5 deg 5 p 3- ھو معامل الحد من الدرجة 2 0 ھو معامل الحد من الدرجة 4 6- ھو معامل الحد من الدرجة 0 2- العملیات على الحدودیات - مجموع حدودیتین ھي حدودیة - جداء حدودیتین ھي حدودیة deg deg deg pq p q - عدد حقیقي في حدودیة ھي حدودیة 5

3-القسمة على a x-a عدد حقیقي خاصیة لتكن p حدودیة من الدرجة 1 n n و a عدد حقیقي توجد حدودیة وحیدة q درجتھا n-1 و عدد حقیقي وحید R بحیث px x aq x R q ھو خارج القسمة الأقلیدیة ل p على x a R ھو باقي القسمة الأقلیدیة ل p على x a ملاحظة pa R فإن px x aq x R كان إذا -1 p a 0 یكافئ p ل جدر a -2 p تقسم x a یكافئ یكافئ باقي القسمة الأقلیدیة ل p على x a ھو 0 المعادلات و المتراجحات من الدرجة الأولى و النظمات 1- المعادلات من الدرجة الأولى بمجھول واحد تعریف a و b عددان حقیقیان معلومان x عدد حقیقي المعادلة من الدرجة الأولى بمجھول واحد حیث المجھول ھو x ھي كل معادلة یمكن كتابتھا على الشكل ax b 0 خاصیة حل المعادلة ax b 0 في ھو - b S a a 0 كان إذا a b 0 0 كان إذا S - a b 0 0 كان إذا S - 2- المتراجحات من الدرجة الأولى بمجھول واحد تعریف ax b ax b ax b ax b lt gt 0 0 0 0 ھي متراجحة من الدرجة الأولى بمجھول واحد a 0 ax b الحدانیة إشارة -3 یعني ax b 0 b x a x b a ax b a إشار عكس 0 a إشار 4 - المعادلات من الدرجة الأولى بمجھولین تعریف a و b و c اعداد حقیقیة معلومة x و y عددان حقیقیان المعادلة من الدرجة الأولى بمجھولین حیث المجھولین ھما x و y ھي كل معادلة یمكن كتابتھا على الشكل ax by c 0 5- نظمة معادلتین من الدرجة الأولى بمجھولین حل النظمة 00 00 a b 1 ax by c x y b a a b محددة النظمة أ - إذا كان 0 فإن النظمة 1 إما لیس مھا حل أو لھا ما لا نھایة من الحلول ب - إذا كان 0 فإن b c y b b c a x a a 6- المتراجحات من الدرجة الأولى بمجھولین quot تجویھ المستوىquot خاصیة quotمقبولةquot y ax by c معادلتھ مستقیم D 00 a b و المستقیم D یحدد نصفي مستوى مفتوحین P P P M x y P ax by c 0 gt P M x y P ax by c 0 lt المعادلات و المتراجحات من الدرجة الثانیة بمجھول واحد I المعادلات من الدرجة الثانیة بمجھول واحد 1- تعریف a و b و c أعدد حقیقیة معلومة 0 a x عدد حقیقي المعادلة من الدرجة الثانیة بمجھول واحد حیث المجھول ھو x ھي كل معادلة یمكن كتابتھا على الشكل 2 ax bx c 0 2 ممیزھا یسمى b ac 4 6

2- مبرھنة المعادلة نعتبر 2 0 a ax bx c 0 ممیزھا و S مجموعة حلولھا في إذا كان 0 lt فإن 2 2 b b S a a 2 إذا كان 0 فإن b S a إذا كان 0 gt فإن S ملاحظة x حلي المعادلة x 2 و 1 إذا كان 2 ax bx c 0 0 a 2 فإن 1 2 ax bx c a x x x x 3- خاصیة x حلي المعادلة x 2 و 1 إذا كان 2 ax bx c 0 0 a فإن 1 2 b x x a 1 2 و c x x a II المتراجحات من الدرجة الثانیة بمجھول واحد التعبیر إشارة 2 0 a ax bx c المعادلة نعتبر 2 یسمى ax bx c 0 ممیزھا x حلا المعادلة x 2 و 1 1- إذا كان 0 lt و 2 ax bx c 0 نفترض 1 2 x x lt x حل المعادلة 2 1- - إذا كان 0 و 2 ax bx c 0 x x 1 a إشارة 0 a إشارة 2 ax bx c 0 فإن lt 0 كان إذا -3 2 لھما a و ax bx c 0 نفس الإشارة الحساب المثلثي I - وحدات قیاس زاویة Cor دائرة وحدات قیاس زاویة ھي الردیان rad الدرجة الغراد gr بوحدة قیاس المسافة AB r بوحدة قیاس المساحة 2 2 S r إذا كان قیاسات نفس الزاویة على التوالي ب الردیان الدرجة الغراد 0 2000 1800 فإن 200 180 تعریف نعتبر الدائرة C O 1 و A و B نقطتان من الدائرة C AOB بالردیان ھو قیاس القوس قیاس الزاویة الھندسیة AB AOB AB AB بوحدة قیاس المسافة بالردیان AOB 0 AOB II الدائرة المثلثیة OII معلم متعامج ممنظم C O 1 الدائرة نعتبر J C و I C في الشكل موجھة C O 1 الدائرة توجیھا موجبا C تسمى الدائرة المثلثیة III الأفاصیل المنحنیة لدائرة IOM rad یسمى أفصولا منحنیا للنقطة M M نرمز x x 1 x 2 a إشارة 0 a إشارة عكس0 a إشارة 2 ax bx c 0 7

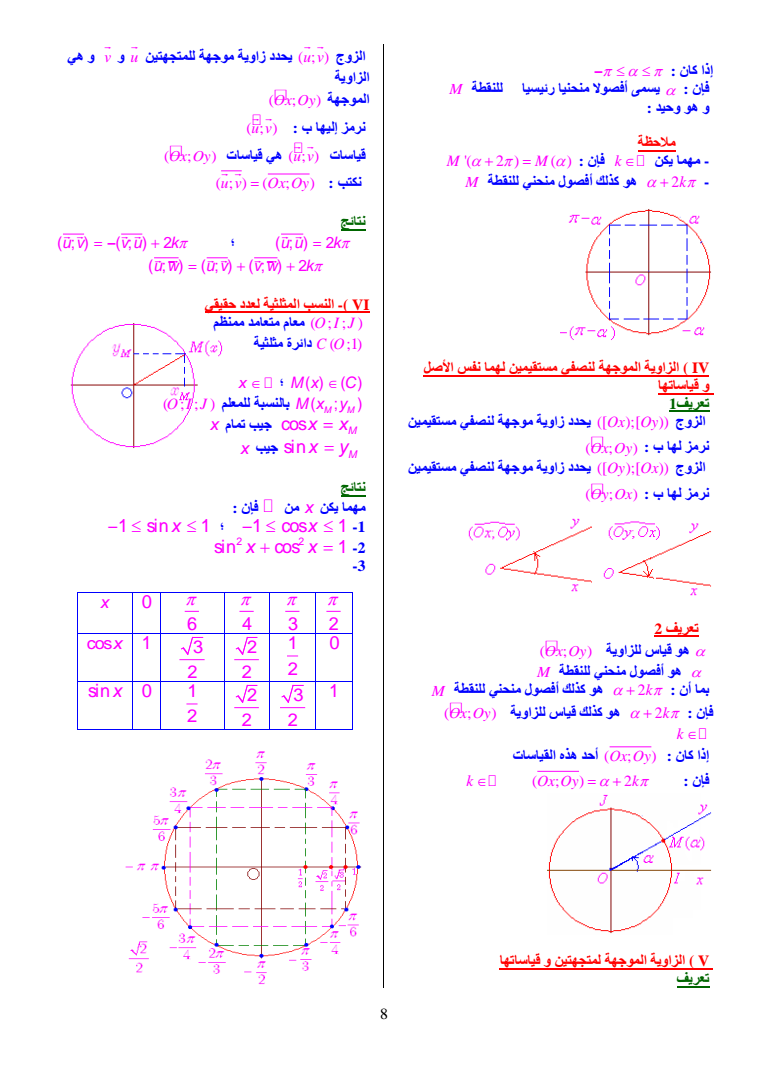
إذا كان فإن یسمى أفصولا منحنیا رئیسیا للنقطة M و ھو وحید ملاحظة M M 2 فإن k یكن مھما - - 2k ھو كذلك أفصول منحني للنقطة M IV الزاویة الموجھة لنصفي مستقیمین لھما نفس الأصل و قیاساتھا تعریف1 الزوج Ox Oy یحدد زاویة موجھة لنصفي مستقیمین نرمز لھا ب Ox Oy الزوج Oy Ox یحدد زاویة موجھة لنصفي مستقیمین نرمز لھا ب Oy Ox تعریف 2 للزاویة قیاس ھو Ox Oy ھو أفصول منحني للنقطة M بما أن 2k ھو كذلك أفصول منحني للنقطة M Ox Oy للزاویة قیاس كذلك ھو 2k فإن k إذا كان Ox Oy أحد ھذه القیاسات k 2 Ox Oy k فإن V الزاویة الموجھة لمتجھتین و قیاساتھا تعریف یحدد زاویة موجھة للمتجھتین u الزوج u v v و و ھي الزاویة Ox Oy الموجھة نرمز إلیھا ب u v قیاسات u v Ox Oy قیاسات ھي u v Ox Oy نكتب نتائج 2 uu k 2 uv vu k 2 uw uv vw k VI - النسب المثلثیة لعدد حقیقي OIJ معام متعامد ممنظم مثلثیة دائرة C O 1 x Mx C Mx y M M OIJ للمعلم بالنسبة cos x x M x تمام جیب sin M x جیب x y نتائج مھما یكن x من فإن 1 sin 1 x 1 cos 1 x -1 -2 2 2 sin cos 1 x x -3 2 3 4 6 x 0 1 0 2 2 2 3 2 cosx 1 3 1 2 2 2 1 2 sinx 0 8

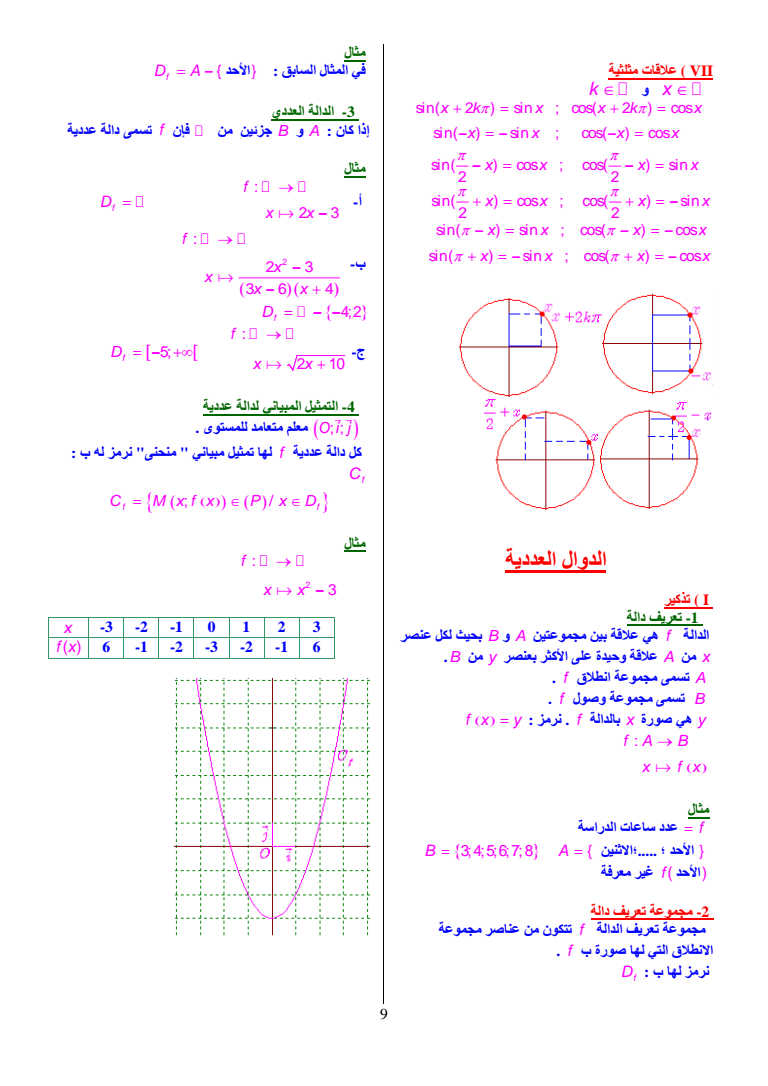
VII علاقات مثلثیة k و x sin 2 sin cos 2 cos xk x xk x sin sin cos cos x x xx sin cos cos sin 2 2 xx xx sin cos cos sin 2 2 xx x x sin sin cos cos xx x x sin sin cos cos xx xx الدوال العددیة I تذكیر 1- تعریف دالة الدالة f ھي علاقة بین مجموعتین A و B بحیث لكل عنصر x من A علاقة وحیدة على الأكثر بعنصر y من B A تسمى مجموعة انطلاق f B تسمى مجموعة وصول f fx y نرمز f بالدالة x صورة ھي y fA B x fx مثال f عدد ساعات الدراسة B 345678 A الاثنین الأحد الأحد f غیر معرفة 2- مجموعة تعریف دالة مجموعة تعریف الدالة f تتكون من عناصر مجموعة الانطلاق التي لھا صورة ب f Df نرمز لھا ب مثال D A f في المثال السابق الأحد 3- الدالة العددي إذا كان A و B جزئین من فإن f تسمى دالة عددیة مثال أ- 2 3 f x x Df ب- 2 2 3 36 4 f x x x x Df 42 ج- 2 10 f x x 5 Df 4- التمثیل المبیاني لدالة عددیة Oi j للمستوى متعامد معلم كل دالة عددیة f لھا تمثیل مبیاني quot منحنىquot نرمز لھ ب Cf C M xf x P x D f f مثال 2 3 f x x x -3 -2 -1 0 1 2 3 f x 6 -1 -2 -3 -2 -1 6 9

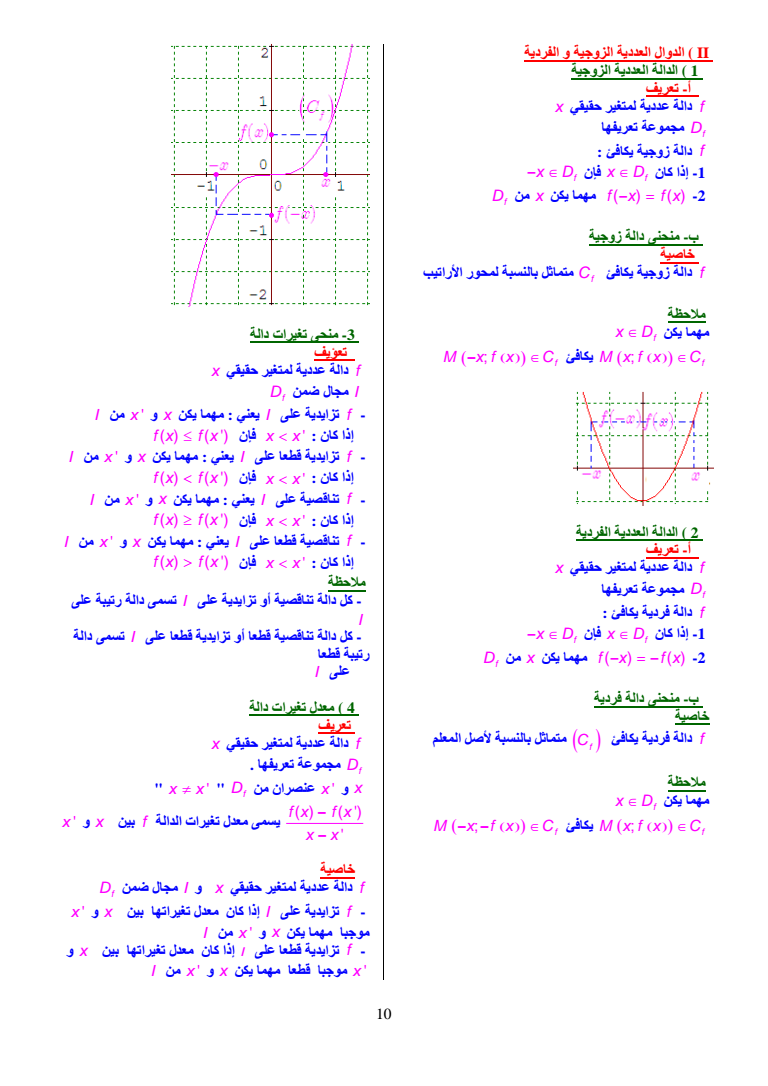
II الدوال العددیة الزوجیة و الفردیة 1 الدالة العددیة الزوجیة أ- تعریف f دالة عددیة لمتغیر حقیقي x مجموعة تعریفھا Df f دالة زوجیة یكافئ كان إذا -1 f x Df فإن x D من x یكن مھما f x fx -2 Df ب- منحنى دالة زوجیة خاصیة متماثل بالنسبة لمحور الأراتیب f Cf دالة زوجیة یكافئ ملاحظة یكن مھما f x D M xf x C f یكافئ M xf x C f 2 الدالة العددیة الفردیة أ- تعریف f دالة عددیة لمتغیر حقیقي x مجموعة تعریفھا Df f دالة فردیة یكافئ كان إذا -1 f x Df فإن x D من x یكن مھما f x fx -2 Df ب- منحنى دالة فردیة خاصیة متماثل بالنسبة لأصل المعلم f Cf دالة فردیة یكافئ ملاحظة یكن مھما f x D M xf x C f یكافئ M x fx C f 3- منحى تغیرات دالة تعؤیف f دالة عددیة لمتغیر حقیقي x I Df مجال ضمن - f تزایدیة على I یعني مھما یكن x و x من I fx fx فإن x x lt كان إذا - f تزایدیة قطعا على I یعني مھما یكن x و x من I fx fx lt فإن x x lt كان إذا - f تناقصیة على I یعني مھما یكن x و x من I fx fx فإن x x lt كان إذا - f تناقصیة قطعا على I یعني مھما یكن x و x من I fx fx gt فإن x x lt كان إذا ملاحظة - كل دالة تناقصیة أو تزایدیة على I تسمى دالة رتیبة على I - كل دالة تناقصیة قطعا أو تزایدیة قطعا على I تسمى دالة رتیبة قطعا على I 4 معدل تغیرات دالة تعریف f دالة عددیة لمتغیر حقیقي x مجموعة تعریفھا Df quot x x quot Df من عنصران x و x fx fx x x یسمى معدل تغیرات الدالة f بین x و x خاصیة f Df دالة عددیة لمتغیر حقیقي x و I مجال ضمن - f تزایدیة على I إذا كان معدل تغیراتھا بین x و x موجبا مھما یكن x و x من I - f تزایدیة قطعا على I إذا كان معدل تغیراتھا بین x و x موجبا قطعا مھما یكن x و x من I 10

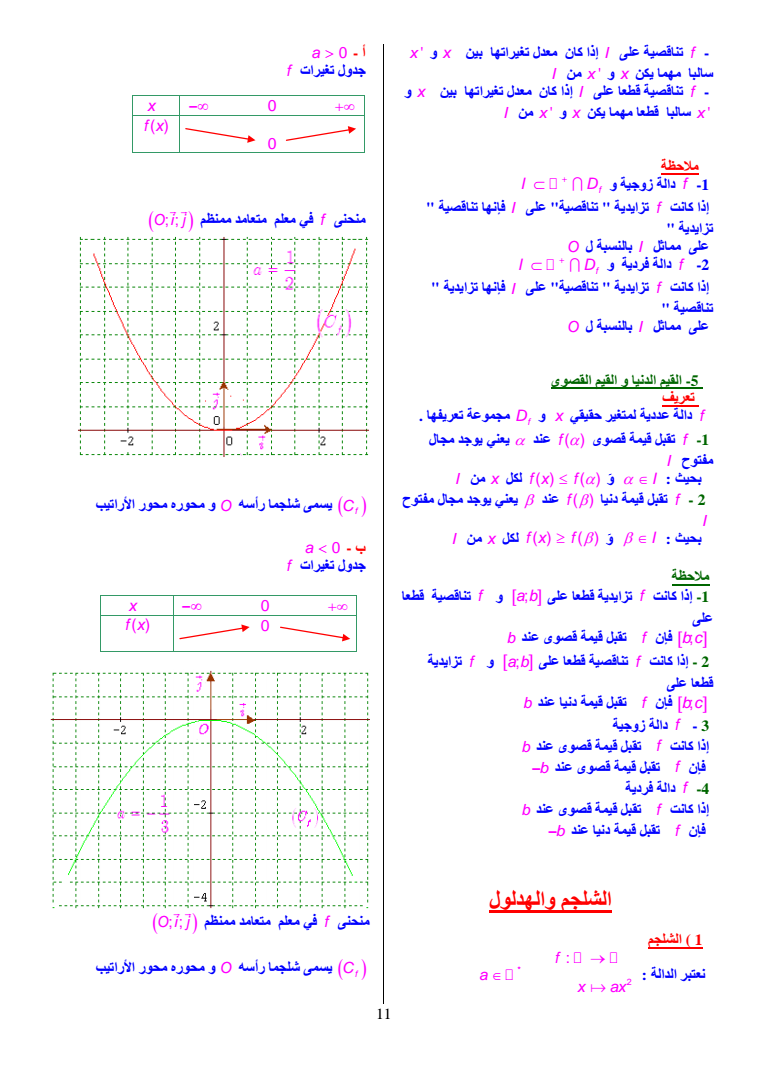
- f تناقصیة على I إذا كان معدل تغیراتھا بین x و x سالبا مھما یكن x و x من I - f تناقصیة قطعا على I إذا كان معدل تغیراتھا بین x و x سالبا قطعا مھما یكن x و x من I ملاحظة I Df و زوجیة دالة f -1 إذا كانت f تزایدیة quot تناقصیةquot على I فإنھا تناقصیة quot تزایدیة quot على مماثل I بالنسبة ل O I Df و فردیة دالة f -2 إذا كانت f تزایدیة quot تناقصیةquot على I فإنھا تزایدیة quot تناقصیة quot على مماثل I بالنسبة ل O 5- القیم الدنیا و القیم القصوى تعریف مجموعة تعریفھا f Df دالة عددیة لمتغیر حقیقي x و f -1 تقبل قیمة قصوى f عند یعني یوجد مجال مفتوح I I بحیث و I من x لكل fx f f - 2 تقبل قیمة دنیا f عند یعني یوجد مجال مفتوح I I بحیث و I من x لكل fx f ملاحظة 1- إذا كانت f تزایدیة قطعا على a b و f تناقصیة قطعا على b c فإن f تقبل قیمة قصوى عند b 2 - إذا كانت f تناقصیة قطعا على a b و f تزایدیة قطعا على b c فإن f تقبل قیمة دنیا عند b f - 3 دالة زوجیة إذا كانت f تقبل قیمة قصوى عند b فإن f تقبل قیمة قصوى عند b f -4 دالة فردیة إذا كانت f تقبل قیمة قصوى عند b فإن f تقبل قیمة دنیا عند b الشلجم والھدلول 1 الشلجم 2 نعتبر الدالة f x ax a a gt 0 - أ جدول تغیرات f منحنى f في معلم متعامد ممنظم Oi j Cf یسمى شلجما رأسھ O و محوره محور الأراتیب a lt 0 - ب جدول تغیرات f x 0 f x 0 منحنى f في معلم متعامد ممنظم Oi j Cf یسمى شلجما رأسھ O و محوره محور الأراتیب x 0 f x 11

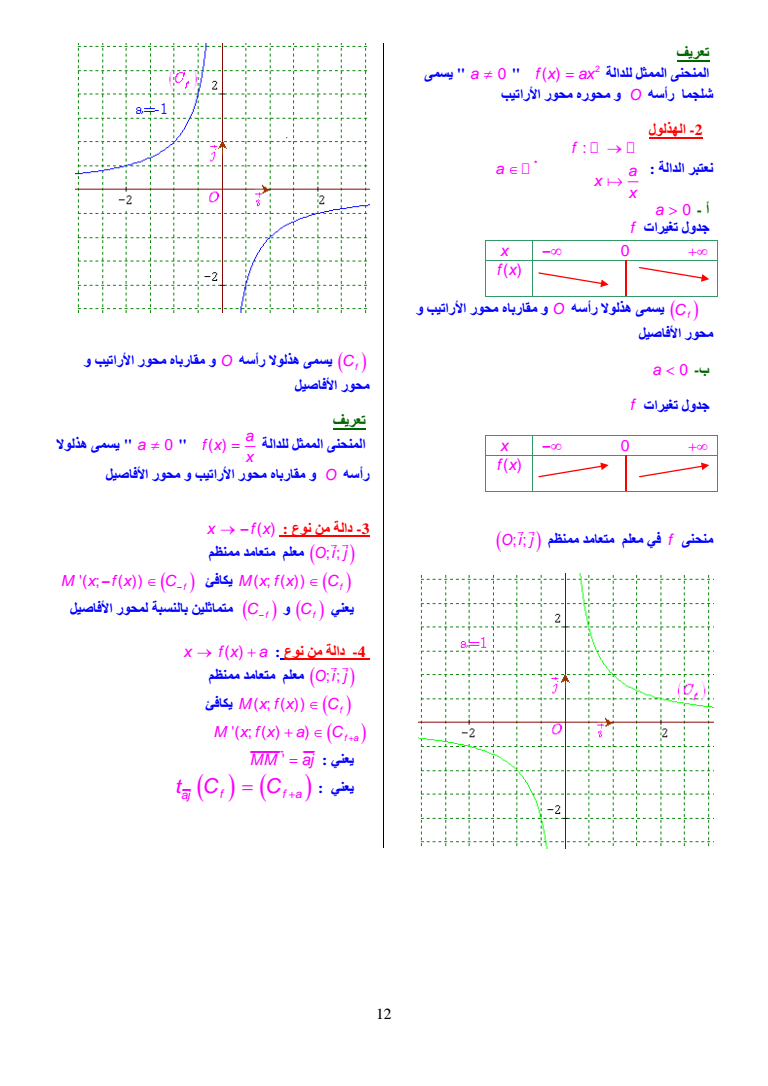
تعریف للدالة الممثل المنحنى 2 یسمى quot a 0 quot f x ax شلجما رأسھ O و محوره محور الأراتیب 2- الھذلول نعتبر الدالة f a x x a a gt 0 - أ جدول تغیرات f x 0 f x یسمى ھذلولا رأسھ O و مقارباه محور الأراتیب و Cf محور الأفاصیل a lt 0 -ب جدول تغیرات f x 0 f x منحنى f في معلم متعامد ممنظم Oi j Cf یسمى ھذلولا رأسھ O و مقارباه محور الأراتیب و محور الأفاصیل تعریف a f x المنحنى الممثل للدالة x quot a 0 quot یسمى ھذلولا رأسھ O و مقارباه محور الأراتیب و محور الأفاصیل 3- دالة من نوع x fx Oi j ممنظم متعامد معلم Mxfx C f یكافئ M x fx C f متماثلین بالنسبة لمحور الأفاصیل Cf و Cf یعني x fx a نوع من دالة -4 Oi j ممنظم متعامد معلم Mxfx C f یكافئ M xfx a C f a MM aj یعني یعني aj f fa tC C 12

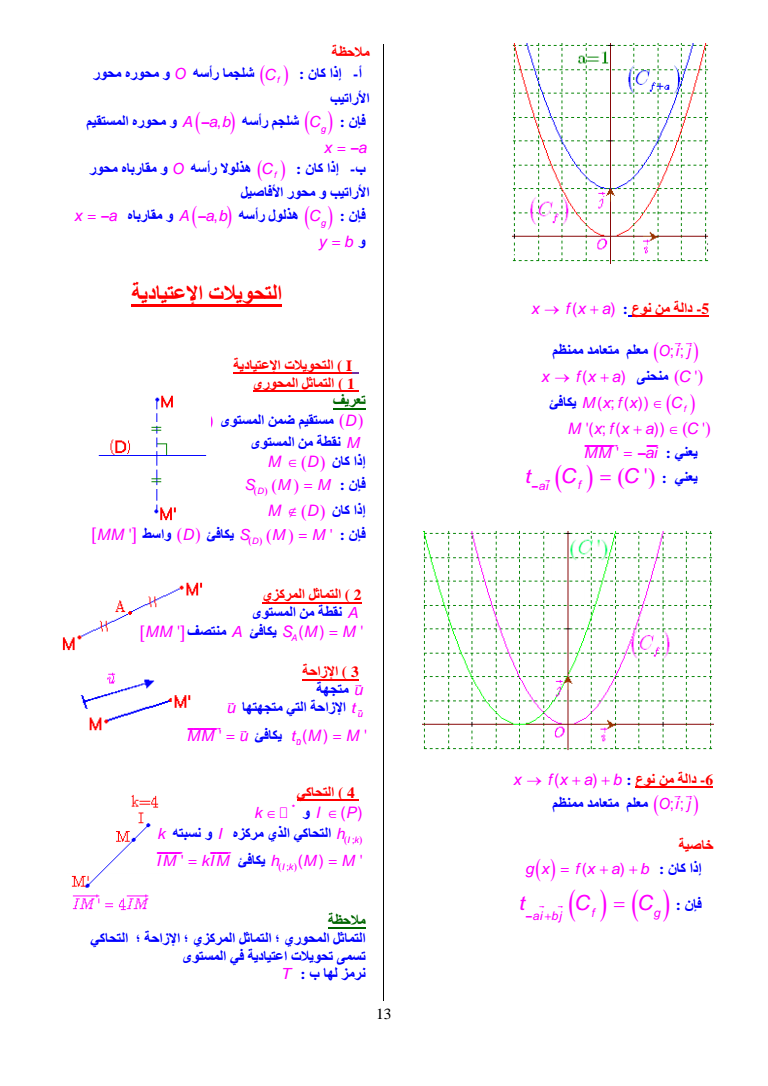
x fx a نوع من دالة -5 Oi j ممنظم متعامد معلم x fx a منحنى C Mxfx C f یكافئ M xfx a C MM ai یعني یعني ai f tC C x fx a b نوع من دالة -6 Oi j ممنظم متعامد معلم خاصیة gx fx a b كان إذا فإن ai bj f g tCC ملاحظة شلجما رأسھ O و محوره محور Cf أ- إذا كان الأراتیب C فإن شلجم رأسھ A ab و محوره المستقیم g x a ب- إذا كان Cf ھذلولا رأسھ O و مقارباه محور الأراتیب و محور الأفاصیل C فإن g ھذلول رأسھ A ab و مقارباه x a y b و التحویلات الإعتیادیة I التحویلات الإعتیادیة 1 التماثل المحوري تعریف D مستقیم ضمن المستوى P M نقطة من المستوى إذا كان M D فإن SM M D إذا كان M D فإن MM واسط D یكافئ SM M D 2 التماثل المركزي A نقطة من المستوى MM منتصف A یكافئ SM M A 3 الإزاحة u متجھة u u متجھتھا التي الإزاحة t u MM u یكافئ tM M 4 التحاكي و I P k h التحاكي الذي مركزه I و نسبتھ I k k IM kIM یكافئ hMM I k ملاحظة التماثل المحوري التماثل المركزي الإزاحة التحاكي تسمى تحویلات اعتیادیة في المستوى نرمز لھا ب T 13

II خاصیات 1- النقط الصامدة ھي SD D أ- النقط الصامدة ب ب- النقط الصامدة ب SA ھي A k 1 I ھي hI k ب الصامدة النقط -ج u u 0 t د لا توجد أي نقطة صامدة ب 2 خاصیات ممیزة TN N و TM M لیكن M N MN یكافئ مركزي تماثل T - أ M N kMN یكافئ تحاكي T - ب M N MN یكافئ إزاحة T -ج 3 استقامیة النقط خاصیة التحویلات الاعتیادیة تحافظ على استقامیة النقط یعني إذا كان C BA نقط مستقیمیة TC C TB B TA A و فإن CBA نقط مستقیمیة 4 توازي مستقیمین خاصیة التحویلات الاعتیادیة تحافظ على توازي مستقیمین یعني T و TD D و D كان إذا D فإن 5 صورة زاویة خاصیة التحویلات الاعتیادیة تحافظ على قیاس زاویة یعني TC C TB B TA A كان إذا ABC A B C فإن 6 تعامد مستقیمین خاصیة التحویلات الاعتیادیة تحافظ على تعامد مستقیمین یعني إذا كان D و TD D و T فإن D 7 صورة مستقیم خاصیة صورة مستقیم بالتحویلات الاعتیادیة التماثل المركزي الإزاحة التحاكي ھو مستقیم یوازیھ یعني hD D SD D A utD D 8 صورة دائرة S C OR C S O R D D S C OR C S O R A A h hC OR C hO kR I k u u t C OR C t O R 9 صورة قطعة خاصیة صورة قطعة بالتحویلات الاعتیادیة التماثل المركزي التماثل المحوري الإزاحة ھي قطعة تقایسھا 10 منتصف قطعة خاصیة التحویلات الاعتیادیة تحافظ على منتصف قطعة یعني AB منتصف I و T AB EF كان إذا EF منتصف T I فإن ملاحظة T -1 تماثل مركزي أو إزاحة أو تحاكي إذا كان و TA B فإن T D E -2 TD T TE یكافئ الجداء السلمي I الجداء السلمي AB متجھتان غیر منعدمتان و AC P BH AC ھو العدد الحقیقي و AC الجداء السلمي ل AB AB AC AH AC AC ل كان إذا AH و نفس المنحى AB AC AH AC AC ل كان إذا AH و منحیان متعاكسان 14

خاصیة u v و متجھتان غیر منعدمتان الزاویة المرتبطة بھما uv uv cos u v 0 منعدما أحدھما كان إذا نتیجة - 2 2 u u u v - u v 0 یكافئ عمودي على جمیع متجھات المستوى 0 - - cos u v u v u v II خاصیات الجداء السلمي uv vu -1 u v w uw vw -2 a u v au v -3 نتائج w u v wu wv 2 2 2 u v u uv v 2 22 2 u v u uv v 2 2 2 2 u v u uv v 2 22 2 u v u uv v 2 2 2 u vu v u v uv w u vw ملاحظة II العلاقات المتریة خاصیة ABC مثلث قائم الزاویة في A P BH AC -1 222 فیتاغورس علاقة quot BC AB AC -2 2 BA BH BC -3 2 AH HB HC IV مبرھنة الكاشي مبرھنة ABC مثلث لدینا 222 BC AB AC AB AC BAC 2 cos V مبرھنة المتوسط مبرھنة A و B نقطتان من المستوى و I منتصف القطعة AB M نقطة من المستوى 2 2 1 4 MA MB MI AB 2 2 MA MB IM AB 2 22 2 2 1 2 2 MA MB MI AB خاصیة1 ABC مثلث 1 sin 2 S AB AC BAC ABC خاصیة2 ABC مثلث 2 S ABC ABC sin sin sin AB AC BC BC AC AB ملاحظة یمكن الاكتفاء ب 2MI MA MB عوضا عن IV و V الھندسة الفضائیة التقاطع والتوازي في الفضاء I المستوى - ثلاث نقط غیر مستقیمیة تحدد مستوى النقط CBA تحدد مستوى نرمز لھ ب ABC - مستقیمان متقاطعان قطعا یحددان مستوى - مستقیمان متوازیان قطعا یحددان مستوى - مستقیم و نقطة خارجھ یحددان مستوى - إذا كان لمستویین مختلفین نقطة مشتركة فھما یتقاطعان في مستقیم یمر من ھذه النقطة II الأوضاع النسبیة لمستقیمین D و D مستقیمان ضمن الفضاء D و D یكونان إما 15

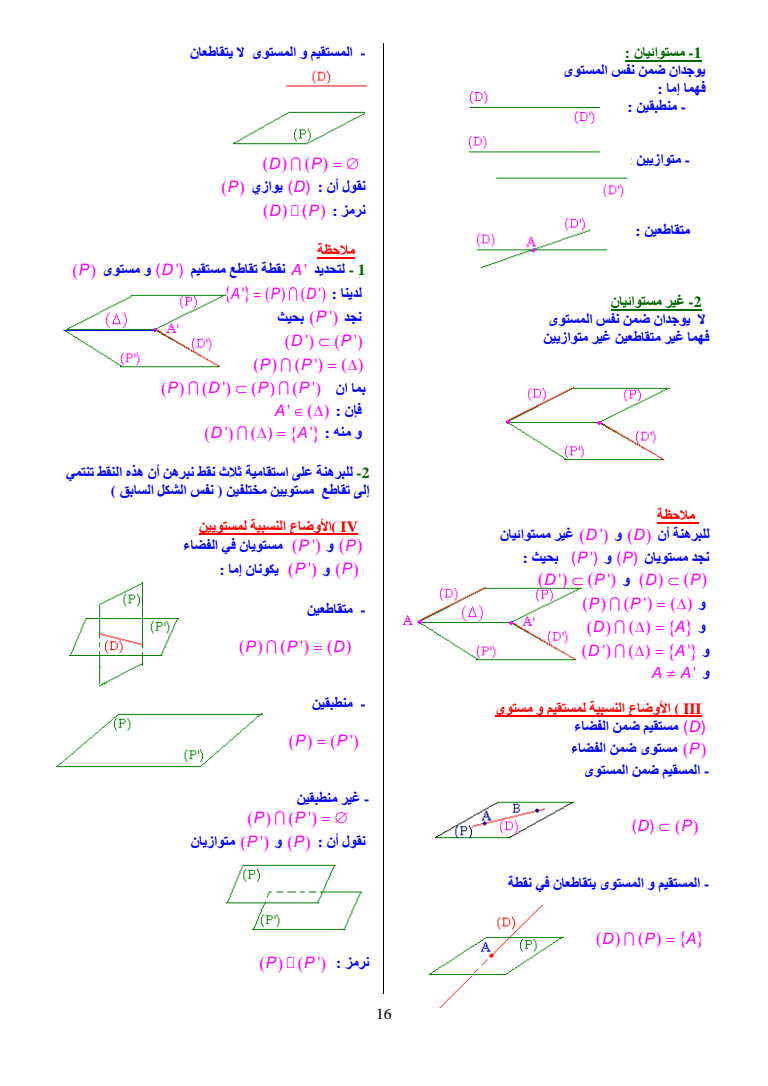
1- مستوائیان یوجدان ضمن نفس المستوى فھما إما - منطبقین - متوازیین متقاطعین 2- غیر مستوائیان لا یوجدان ضمن نفس المستوى فھما غیر متقاطعین غیر متوازیین ملاحظة للبرھنة أن D و D غیر مستوائیان نجد مستویان P و P بحیث D P و D P P P و D A و D A و A A و III الأوضاع النسبیة لمستقیم و مستوى D مستقیم ضمن الفضاء P مستوى ضمن الفضاء - المسقیم ضمن المستوى D P - المستقیم و المستوى یتقاطعان في نقطة DPA - المستقیم و المستوى لا یتقاطعان D P نقول أن D یوازي P D P نرمز ملاحظة 1 - لتحدید A نقطة تقاطع مستقیم D و مستوى P A PD لدینا نجد P بحیث D P P P PD PP ان بما فإن A D A منھ و 2- للبرھنة على استقامیة ثلاث نقط نبرھن أن ھذه النقط تنتمي إلى تقاطع مستویین مختلفین نفس الشكل السابق IV الأوضاع النسبیة لمستویین P و P مستویان في الفضاء P و P یكونان إما - متقاطعین PP D - منطبقین P P - غیر منطبقین P P نقول أن P و P متوازیان P P نرمز 16

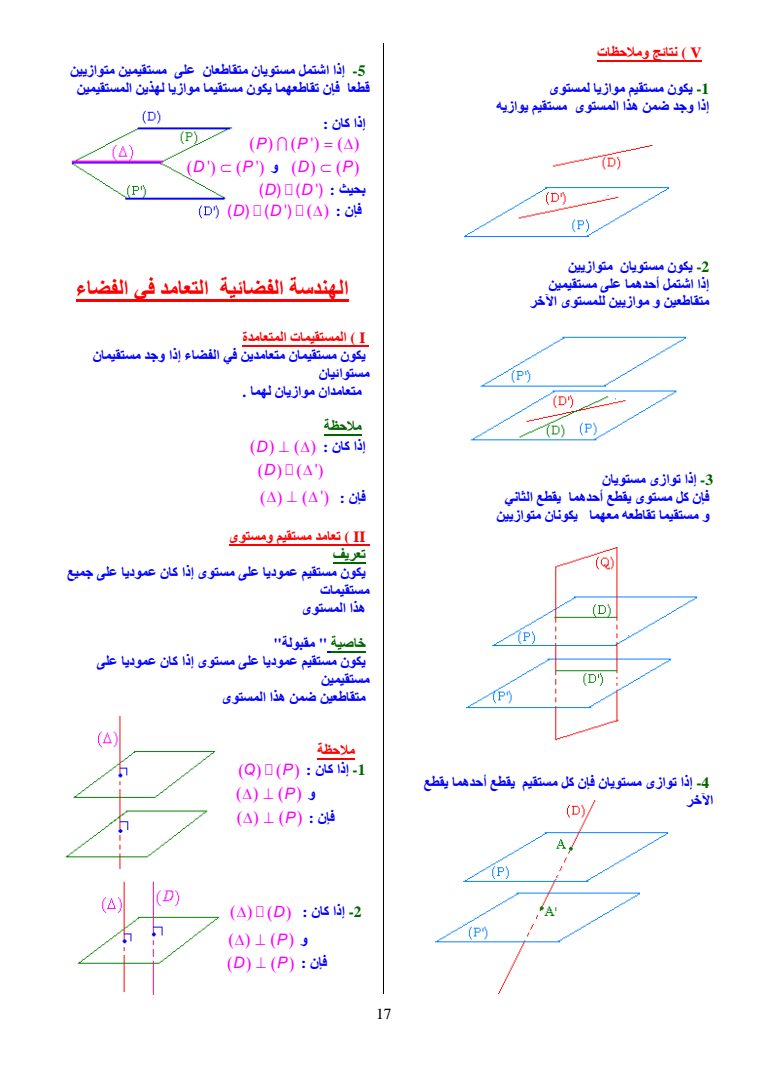
V نتائج وملاحظات 1- یكون مستقیم موازیا لمستوى إذا وجد ضمن ھذا المستوى مستقیم یوازیھ 2- یكون مستویان متوازیین إذا اشتمل أحدھما على مستقیمین متقاطعین و موازیین للمستوى الآخر 3- إذا توازى مستویان فإن كل مستوى یقطع أحدھما یقطع الثاني و مستقیما تقاطعھ معھما یكونان متوازیین 4- إذا توازى مستویان فإن كل مستقیم یقطع أحدھما یقطع الآخر 5- إذا اشتمل مستویان متقاطعان على مستقیمین متوازیین قطعا فإن تقاطعھما یكون مستقیما موازیا لھذین المستقیمین إذا كان P P D P و D P D D بحیث D D فإن الھندسة الفضائیة التعامد في الفضاء I المستقیمات المتعامدة یكون مستقیمان متعامدین في الفضاء إذا وجد مستقیمان مستوائیان متعامدان موازیان لھما ملاحظة إذا كان D D فإن II تعامد مستقیم ومستوى تعریف یكون مستقیم عمودیا على مستوى إذا كان عمودیا على جمیع مستقیمات ھذا المستوى خاصیة quot مقبولةquot یكون مستقیم عمودیا على مستوى إذا كان عمودیا على مستقیمین متقاطعین ضمن ھذا المستوى ملاحظة Q P كان إذا -1 و P فإن P D كان إذا -2 و P D P فإن 17

III تعامد مستویین تعریف یكون مستویان متعامدان إذا وجد ضمن أحدھما مستقیم عمودي على الآخر ملاحظة تعامد مستویین لا یعني بالضرورة أن كل مستقیم ضمن أحدھما عمودي على الآخر 18