الامتحانات الوطنية مع التصحيح من 2003 الى 2009





J AK P 14AK 2 2009 J K K P X H A J AK Q Aj J B iJ j K Q m H AJ J B K Q J F Mx y x y 1 x M2Rx y R R j F o J M2R Q J Z Qk F J J - 1 A JK Y F Ma b Mx y o J Mx y Ma b x y 1 x a b 1 a xa xb y a 1 xa Mxa xb y a M2R Q J Z Qk F J J XAJ K Q Q P F J J H F aJ m A M2R aJ m M2R Q J Z Qk F A 1 F J AK F YK Aj Q Ja I M1 0 F A JK Y 2 F J AK KA M 1 x y J K F Mx y Q J 3 XA A J A JK Y F XAJ K Q 4 M1 1 M2 3 1 1 0 1 2 3 1 2 2 7 2 1 2 M2 3 M1 1 2 3 1 2 1 1 0 1 2 5 1 2 M1 1 M2 3 6 M2 3 M1 1 J F J K Q k Q P G J J G Mx 0 Fx R o J - 2 I G B G 6 A JK Y 1 Mx 0 Ma 01 Mx 0 M 1 a 0 M x a 0 A JK Y R a x oJ 2 E R R oJ - 3 x y E a b E x ya b xa xb y a gY I J Q KA K E X Q K F 7 E Mx y 7 x y J J J Q Ja K 1 12 3 2 7 2 2 31 1 2 5 A JK Y F K Q J Ma b Mx y o J A J J 1 H 1 H m I k Mx y Ma b Mxa xb y a J KA K k 12 Y A JK Y J Mxa xb y a xa xb y a x ya b Mx yMa b Mx y Ma b Mx yMa b

J AK P 14AK 2 2009 J K K P X HA J AK Q Aj J B iJ j K A K J J 2 Mx y x y IJ m F Mx y YJ k XY m E x y h P Q P E X K Q m J J K A F E i J J K A h J XAJ K Q K Y a XY B GA J K Q J m 6 1 IJ m Y X Y m E z 2 1 i1 mz im2 1 0 XAa C j Q Ja K I 1 im 12 j J J 1 1 i1 m2 4im2 1 A JK Y A 1 i 2 2i 1 i 2 2i A 2im2 2m 1 1 i 2 m 12 1 im 12 E XAa C j J H z1 1 i1 m 1 im 1 2 1 im A g J K E z2 1 i1 m 1 im 1 2 m i z1z2 1 1 imm i 1 im2 1 1 h m2 1 i m2 1 i J A J S J Z A34 K iJ m2 1 i K A m x iy A PA B K A y x A S x 2 y 2 1 x 2 y 2 2 2xy 1 x 2 2 1 2 y 2 2 1 2 2xy 1 m r 2 1 2 i r 2 1 2 m r 2 1 2 i r 2 1 2 A JK Y 2 lt lt m e i Ag 2 z1 1 im 1 e i 2 e i 2 4 e i 2 4 e i 2 4 2 cos 2 4 e i 2 4 J 0 lt 2 4 lt 2 A 2 lt lt A z1 2 cos 2 4 cos 2 4 isin 2 4 z2 m i e i e i 2 e i 2 4 e i 2 4 e i 2 4

J AK P 14AK 2 2009 J K K P X H A J AK Q Aj J B iJ j J 2 lt 2 4 lt A 2 lt lt A z2 2e i 2 3 4 cos 3 4 2 2 cos 3 4 2 cos 2 3 4 isin 2 3 4 M2z2 M1z1 Mm J Q Ja K II 1 im m i R z1 m z2 m R A X X J J M2 M1 M J o K 1 i m im R M2 M1 M IJ m M J m J x y Rx y 6 1 0 m x iy JXA a J 1 y x 0 i x iy ix iy R m J J A1 0 J Qm 1 y x 0 z 0 1 iz IJ m M0 z Mz o J 2 J 1 i 1 2 i 2 m A m YA K J K R K j J A JK Y z C z 6 z z i J z 0 1 iz z 0 iz X 3M M0 2 2M0 M A i J J 1 2 i 2 j H X J o J 2 JK P AJ QQ PX R m x iy H z2 z1 z2 m IR m i 1 im m i m IR ix iy i 1 ix y IR y 1 x 0 Rem Imm 1 Q K X Yg K J K Q A MM1 I J J z1 1 im RM M1 A JK Y h MM1 I JAK J j Q K Y A D Q MM1 IJ m M M1 Q YJ k C K Q A M2MM1 Z A34K M2 C Z A34K PY J M2 M M1 J o K J z2 z1 z2 m IR Z A34K arg z2 z1 z2 m 2 2 Z A34K 3 M2M M2M1 2 2 Z A34K M2 Rem Imm 1 K A I k Z A34K JXAa Y J PY J M2 M M1 m Mm J m X A1 0 J Qm x y 1 0 H AJ K Am I A J K Q J an 2 n 3 n 6 n 1 N n 34 k P X Y an N n 34 K j J J 1 2 02 n N 2 n 02 3 12 n N 3 n 12 httpmathkasicima

J AK P 14AK 2 2009 J K K P X H A J AK Q Aj J B iJ j 6 02 n N 6 n 02 n N an 2 n 3 n 6 n 1 1 1 02 J k P X Y an N n 34 X 2 13 n N 2 n 1n 3 an 03 A g oK n XY j J H 3 03 n N 3 n 03 6 00 n N 6 n 03 k P X Y n A X X n N an 2 n 3 n 6 n 1 1n 1 03 J p gt 3 IJ m A J X Y p oJ 2 Fermat J Q I k KA p Z 6 1 p Z 2 p Z 3 1 A p p gt 3 A 6 p1 1p 2 p1 1p 3 p1 1p i J J K A 6ap2 3 2 p1 2 3 p1 6 p1 6 A JK YK 6ap2 32p1 23p1 6 p1 6 3 2 1 6 0p pap2 GAUSS J Q I k A p Z 6 1 A p6ap2 J A J X Y q oJ h n k J ak Z q q kN qak 1 q 2 I Am n 2k J a2k Z q q kN qa2k H 1 q 3 II Am n q 2 J aq2 Z q q qaq2 H 2 q gt 3 III Am J j J A A X fnx x1 lnxn K A Qa fn 0 7 R Y Q Ja K N n oJ fn0 0 x gt 0 Oij J YAa J a A A Jj J Cn B Z Q m Q J fn A 1 fn0 lim x0 fnx J J m t n x K lim t0 tlnt 0 B lim x0 fnx lim t0 t n 1 nlntn lim t0 t ntlntn 0 fn0

J AK P 14AK 2 2009 J K K P X H A J AK Q Aj J B iJ j Q J fn A J J K A H lim x0 fnx fn0 x 0 I j J Q fn X lim t0 lnt B lim x0 fnx fn0 x 0 lim x0 1 lnxn A JK Y Q J A J C K A lim x f1x x lim x 1 lnx lim x f1x lim x x1 lnx h lim x f2x x lim x 1 lnx2 lim x f2x lim x x1 lnx2 f1 H Q a K 2 x gt 0 f 1 x 1 lnx 1 lnx R A J C K A f1 A JK Y f1 H Q a K Yg x 0 1 f 1 x k 0 f1x 0 1 amp f2 H Q a K H 2 R A J C K A f2 A JK Y x gt 0 f 2 x 1 lnx2 2x 1 x 1 lnx lnx 11 lnx x 0 e 1 e f 2 x k 0 0 f2x 0 4e 1 amp 0 C2 C1 PX 3 x R f1x f2x x1 lnx1 1 lnx xlnx1 lnx x 0 1 e f1x f2x 0 0 0 C1 C2 C2 C1 C1 C2

J AK P 14AK 2 2009 J K K P X H A J AK Q Aj J B iJ j GA J Z Q m x 0 Fx Z 1 e x f1t 1 t 2 dt IJ m F Y Q Ja K 1 A J C K A u x 7 e x Y 0 J t 7 f1t 1 t 2 Y A J C K A F J u 0 0 x lt 0 F x e x fe x 1 e 2x e x e x 1 lne x 1 e 2x e 2x x 1 1 e 2x J A J K F H J 0 f1t t e x 1 2 1 t 2 1 e 2x A JK Y 0 x oJ 2 J t e x 1 1 2 f1t 1 1 t 2 f1t 1 1 e 2x f1t Z 1 e x 1 2 f1tdt Z 1 e x 1 1 t 2 f1tdt Z 1 e x 1 1 e 2x f1tdt 1 2 Z 1 e x f1tdt Fx 1 1 e 2x Z 1 e x f1tdt x 2 3 4 lnx 2 f1x A JK Y 0 x 34 H 2 A lim x e 2x 3 4 x 2 A Z 1 e x f1tdt t 2 3 4 lnt 2 1 e x 3 4 e 2x 3 4 x 2 h lim x Z 1 e x f1tdt 3 4 3 8 l 3 4 i J J H 2 3 I A J Z Q m un Z e 1 fntdt N n 34 un Z e 1 fntdt 0 J x 1 e fnx 0 A JK Y N n oJ 1 A JK Y 1 e x oJ H A JK Y fn1x fnx x1 lnxn 1 lnx 1 xlnx1 lnxn 1 x e 0 lnx 0 1 lnx 0 1 lnxn x 1 e fn1x fnx 0 J m 1 e fn1 fn 0 KA J A34 K A n N oJ k un1 un h 1 I k J A J K 1 I k Q AK P a un X httpmathkasicima

J AK P 14AK 2 2009 J K K P X H A J AK Q Aj J B iJ j u x x vx 1 lnxn1 n N oJ 2 ux x 2 2 v x n 11 lnxn x J un1 Z e 1 x1 lnxn dx x 2 2 1 lnxn1 e 1 n 1 2 Z e 1 x1 lnx n dx n 1 un1 1 2 n 1 2 un A D JXAa K Y J J C2 C1 K Pj J Q g kA A o J H Q J AK x e x 1 J A Z e 1 f2x f1xdx 4cm2 u1 u2 4cm2 A 2cm2 J u1 u2 1 2 2 I k A JK Y I k A un 1 n 1 n 1un 1 2un1 2 I k n 2 34 3 un 1 n 1 X un 1 n 1 A un1 0 1 A J A J K un A 2un1 1 n 1un 2 I k n 2 34 A JK Y A JAK un 1 n 1 J n 1un 2un 1 J 2un1 1 2un 1 1 n 1 un 1 n 1 lim n nun 1 lim n un 0 i J J K A H n 1 dn vn un n N vn1 1 2 n 1 2 vn v1 a a 6 u1 IJ m a R 4 n 1 dn n 2 n1 d1 k Q AK J J d1 d1 n 1 g A JK Y A JK Y dn n 2 n1 d1 Q K n 1 oJ dn1 vn1 un1 n 1 2 vn un n 1 2 dn n 1 2 n d1 J n 1 dn1 dn n 1 2 i J J K A H A dn 2 n3d3 m k Q AK n 3 n 1 2 2 dn1 dn 2 lim n dn A lim n 2 n3d3 K PA J o J dn A dn vn un K PA J un A K PA J vn I KA X h A J K Y XPQD httpmathkasicima



pKctKcKRKVJ aJrJKTJnT 2008 KcKRaKuJcaJ KJCbKTjJ UJiJicRkaKjJaMTJKVJ نقطة 325 CJhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhcTJ M حلقة واحدية 2 M فضاء متجهي حقيقي 2 جسم تبادلي نضع 1 0 0 1 I و 0 3 1 0 3 J 2 و 3 1 3 a b E M a b a b b a J M 01 و I M 10 أن لاحظ 1 أ- لدينا 00 لأن E 9 0 0 0 0 M E E M2 9 وليكن E من عنصرين B و A ليكن 9 2 إذن 2 a b A M a b 2 a b B M c d 3 3 3 1 1 1 3 3 3 a b c d a c b d b a d c b d a c A B A B M a c b d E 2 M وبالتالي فإن E فضاء متجهي جزئي من الفضاء المتجهي الحقيقي ب- لنبين أن I J أساس في الفضاء المتجهي الحقيقي E من a b لكل 9 2 لدينا 1 0 0 1 0 3 1 0 3 M a b a b aI bJ إذن I J أسرة مولدة للفضاء الحقيق E لدينا I J 9 2 أسرة حرة في E لأن لكل a b من 0 0 0 0 0 0 0 3 1 3 aI bJ M a b a b a b b a و E الحقيقي المتجهي الفضاء في أساس I J فإن وبالتالي 2 E a aI bJ b hhhhhhhhhhhhpKctKcKRKVJ 1 nJ

E بما يلي نحو E E 0 M 0 نعتبر التطبيق f المعرف من 2 ليكن f E a ib M a b 6 E من عنصرين B c I dJ و A aI bJ نعتبر -أ 2 لدينا 0 3 0 3 0 1 1 1 0 0 1 0 3 3 J I إذن 2 A B aI bJ cI dJ acI ad bc J bdJ ac bd I ad bc J E 2 M وبالتالي فإن E جزء مستقر من M a b M c d M ac bd ad bc ملاحظة آان إذا -ب 2 فإن z a ib a b معرف تطبيق f فإن ومنه f z M ab E ليكن 9 2 و z a ib a b 2 لدينا z a ib a b z z f aa bb i ab a b z z M aa bb ab a b z z M a a M b b z z f z f z f f f f E نحو ومنه فإن f تطبيق تشاآلي من A E بما أن I J أساس في الفضاء المتجهي الحقيقي E فإن 9 نعتبر 2 ولدينا a b A aI bJ M a b f a ib إذن A E a i b فإن وبالتالي تقابلي تطبيق f إذن A E z f z A E نحو خلاصة f تشاآل تقابلي من 3 لدينا E 9 فضاء متجهي حقيقي إذن E زمرة تبادلية E 9 جزء مستقر من M2 و M2 حلقة واحدية ومنه نستنتج أن القانون تجميعي في E القانون توزيعي على القانون في E وهذا يدل على أن E حلقة واحدیة I هو العنصر المحايد بالنسبة للقانون في E E إذن نحو 9 لدينا f تشاآل تقابلي من E ولدينا A E A 0 0 A 0 يستلزم أن القانون تبادلي في القانون تبادلي في إذن قانون تبادلي في E E زمرة E فإن نحو زمرة تبادلية و f تشاآل تقابلي من 9 بما أن وبالتالي فإن E جسم تبادلي hhhhhhhhhhhhpKctKcKRKVJ 2 nJ

المعادلة E في لنحل 4 3 لدينا J X I 1 3 1 3 1 1 1 3 3 J X f I f J f X f I J X I J X I f أن وبما 1 1 f J f M i 01 0 1 i و 1 1 f I f M 10 0 1 i 1 فإن المعادلة السابقة تصبح 1 f X z و 3 3 3 3 3 3 3 1 1 1 J X I iz z i z i z i z J X I j j i حيث 1 3 2 2 و j i 1 3 2 2 إذن j i 3 3 J X I z i ij i j J X I X f z f i f ij f i j ولدينا 0 3 01 1 0 3 f i M J و 3 3 3 1 3 1 2 2 2 2 2 2 1 3 2 3 2 f ij f i M و 3 3 3 1 3 1 2 2 2 2 2 2 1 3 2 3 2 f i j f i M J X I في E هي 3 وبالتالي فإن مجموعة حلول المعادلة 3 3 3 3 0 3 2 2 2 2 1 0 1 3 1 3 3 2 3 2 2 2 3 S hhhhhhhhhhhhpKctKcKRKVJ 3 nJ

نقطة 375 C hhhhhhhhhhhhhhhhhhhhhKVJhhhhhhhhhhhhhhhhhhhhhcTJ a ليكن المعادلة المجموعة في نعتبر I 2 G iz aai z a iaa 0 1 أ- مميز المعادلة G هو 2 2 2 2 2 2 2 2 2 4 4 4 2 4 2 ac aai i a iaa a i a i a i a a i a a a i a i a a i a a i a a a i a b a 2 ب- مميز المعادلة G هو a i a إذن للمعادلة G حلين عقديين هما 1 2 2 2 i a aai a a i a i i z و 2 1 2 2 2 2 ia aai a a i a i i i z ومنه فإن مجموعة حلول المعادلة G هي S i a1ia G للمعادلة حل a a i a أو a i 1 a 2 1 1 1 2 1 a i m a m a i e a i a e a m a i m a e e a أو a أو I I R R I I R R O u v مباشر ممنظم متعامد معلم إلى منسوب العقدي المستوى II JJG J G Re a m I a أن نفترض A و B و C نقط ألحاقها على التوالي a و i a و 1ia 1 نضع 1 ia a i a a Z أ- لدينا 1 1 1 i a a i i a i a ia a a i i i a a ia a i a i a i a a Z -ب c A B A z z z z A و B و C نقط مستقيمية Z Z Z hhhhhhhhhhhhpKctKcKRKVJ 4 nJ

2 1 1 1 1 1 1 1 0 1 1 1 1 1 2 2 2 1 2 ia a i a i i a a i a a ia a i a i a i i a i i a a i i a a i i i m a i m a i m a I I I 2 1 نفترض في هذا السؤال أن 2 Im a تذآير ليكن R الدوران الذي مرآزه وزاويته ولتكن M z و M z نقطتين من المستوى العقدي 1 M M i i R z e z e الدوران الذي مرآزه A وزاويته R1 نعتبر 2 2 و R2 الدوران الذي مرآزه A وزاويته نضع و R B 1 B BC القطعة منتصف E النقطة لتكن R C2 C لدينا -أ إذن R B 1 B 2 2 1 1 1 i i b e b e a i i a i a i a a ولدينا إذن R C2 C 2 2 1 1 1 i i c e c e a i ia i a i aaia i ia 2 إذن ب- لدينا E منتصف القطعة BC 1 2 b c e i a aff a E i arg 2 إذن c b AE B C e a JJJJGJJJJJJG ولدينا 2 2 1 2 2 1 1 2 1 2 2 2 2 2 i ia a ia a i ia i a a i iaaa i i a ia ia i a a ia i a a a c b e a 2 إذن 2 AE B C JJJJG JJJJJJG 2 و B C c b AE e a B C 2AE و B C AE إذن hhhhhhhhhhhhpKctKcKRKVJ 5 nJ

نقطة 3 C WKVJhhhhhhhhhhhhhhhhhhhhhcTJ المجموعة في نعتبر I 2 E 35u v 96 1 التالية المعادلة E للمعادلة خاص حل 114 إذن 3511 96 4 385384 1 لدينا 1 35 96 1 بينهما فيما أوليان 35و 96 أن نستنتج Bezout حسب 3511 96 4 1 لدينا 2 35u v 11 96 4 i 3596v 4 35 4 Gauss v kvk 4 35 ii k v k 4 3 5 u 11 96k يكافئ u 11 96k أي 35u 11 9635k فنجد i العلاقة في ii العلاقة نتيجة نعوض وبما أن الأزواج 1196k k 435 حيث k تحقق المعادلة E فإن مجموعة حلول المعادلة E هي S k 11 96 4 35k k التالية المعادلة المجموعة في نعتبر II 35 F x 2 9 7 1 ليكن x حلا للمعادلة F أ- لدينا p gt 97 أو gt 2 q p إذن 97 عدد أولي نتوقف إذا آان d 97 أن نفترض d 97 أو d 1 فإن ومنه أولي عدد 97 و d 97 إذن 97 x d لبكن x 079 أي 97 x فإن وعليه 97 x 97 إذن يستلزم وهذا 35 x 0 9 7 ولدينا 35 x 2 97 0 2 97 إذن تناقض وهذا 0 2 أن إلى يشير وهذا 0201297 و وبالتالي فإن 97 97 x 1 و x أوليان فيما بينهما hhhhhhhhhhhhpKctKcKRKVJ 6 nJ

96 x 1 97 ب- لدينا 97x 1 و 97 عدد أولي حسب مبرهنة فيرما لدينا ج- بما أن 35 x 2 97 فإن 11 35 11 x 2 97 i x 385 211 97 أي إذن 3859641 ولدينا 4 385 96 4 1 96 x x x لدينا و 4 4 96 96 4 96 385 x 1 97 x x 1 97 x x 97 x x 97 ii أن نستنتج ii و i من 11 x 2 9 7 بحيث طبيعيا صحيحا عددا x ليكن 2 11 x 2 9 7 إذن 35 11 35 x 2 97 فإن ومنه 35 385 x 2 9 7 أي 4 35 96 x 2 2 9 7 لدينا فيرما مبرهنة حسب فإنه 972 1 و أولي 97 أن وبما 96 2 1 97 إذن 4 96 2 197 أن نستنتج ومنه 35 x 2 9 7 F للمعادلة حل x أي لدينا 3 11 F x 2 97 أن وبما 11 فإن 2 2 048 97 21 11 11 2 11 97 F x k 11 97 1 x 1 97k فإن عليه وبناء نقط 10 C vhhhhhhhhhhhhhhhRJcJhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhcTJ 2 بما يلي I لتكن f الدالة العددية للمتغير الحقيقي x المعرفة على 2 x f x x e O i j JG JGJ وليكن C المنحنى الممثل للدالة f في معلم متعامد ممنظم -أ 1 2 lim 2 0 lim x t lim x x t f x x e e حيث 2 و t x x t ومن نستنتج أن C يقبل مقاربا مائلا بجوار معادلته y x 2 x ليكن -ب لدينا 2 2 2 2 2 2 2 1 0 x x x f x x e xe e gt معرفة من المجال 1 f إذن f تقبل دالة عكسية ج- لدينا f متصلة وتزايدية قطعا على المجال 0 0 0 lim 10 x f f f x نحو المجال 0 فإن المعادلة f x 0 تقبل حلا وحيدا في المجال 0 وبما أن 0 1 0 hhhhhhhhhhhhpKctKcKRKVJ 7 nJ
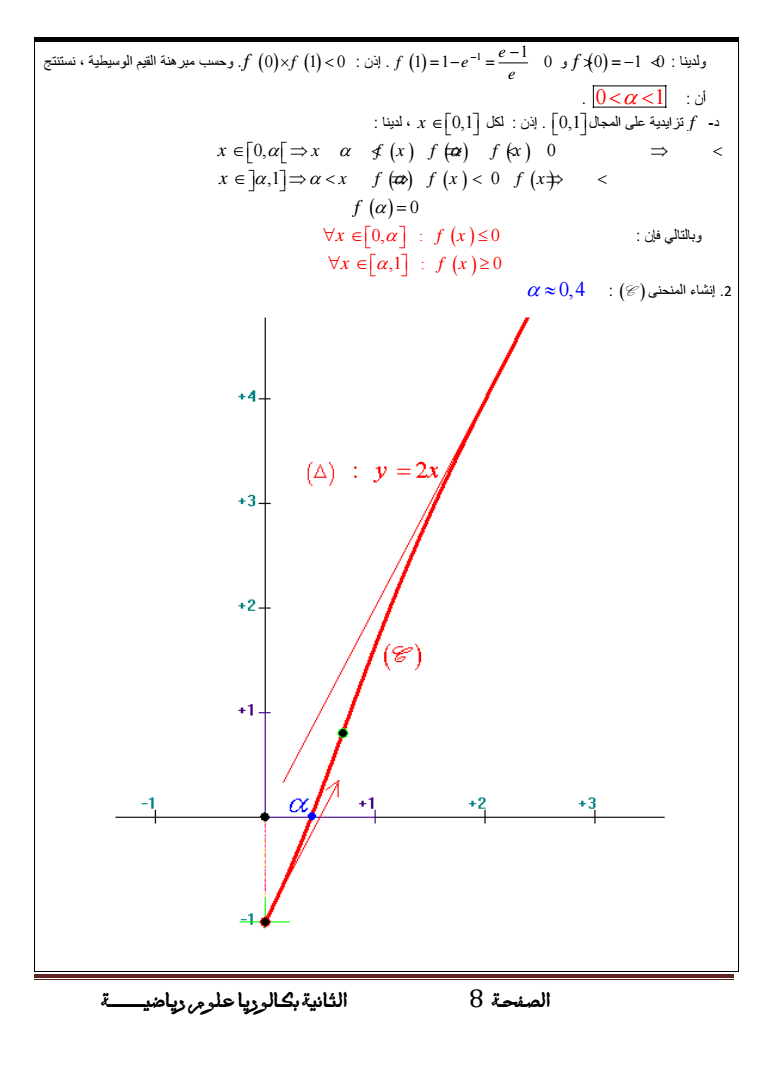
و f 0 1 lt0 ولدينا 1 1 1 1 0 e f e e lt إذن f 0 1 lt f 0 وحسب مبرهنة القيم الوسيطية نستنتج 0 1 lt lt أن لدينا إذن لكل x 01 د- f تزايدية على المجال 01 x 0 x f x f f x 0 lt lt lt x 1 x f f x 0 f x lt lt lt f 0 x 0 f x 0 فإن وبالتالي x 1 f x 0 04 C المنحنى إنشاء 2 hhhhhhhhhhhhpKctKcKRKVJ 8 nJ

بما يلي II نعتبر الدالتين العدديتين و g للمتغير الحقيقي x المعرفتين على 2 2 x t g x x e dt و 2 1 0 0 1 x t x e dt x x gt 1 أ- الطرقة الأولى 2 ليكن x gt 0 نعتبر الدالة حسب خاصية القيمة المتوسطة لدينا دالة متصلة على المجال x x e 6 0x 2 لدينا 1 0 0 x t x c e dt x c أي 2 2 1 0 x t c x e dt e x c الطریقة الثانية 2 نضع x t x F x e dt لدينا F دالة متصلة على 0x وقابلة للاشتقاق x ليكن وقابلة للاشتقاق على F دالة متصلة على 0x على c F 0 x x F F 0 0 c x أن نستنتج المنتهية التزايدات هنة مبر حسب 2 ولدينا u u F u e إذن 2 c F c e فإن ومنه 2 c F x e x أي 2 2 x t c e dt e x فإن وبالتالي 2 2 1 0 x t c x c x e dt e x 1 2 2 ب- من أجل x 1 حسب السؤال السابق لدينا 0 01 t c c e dt e ولدينا 2 2 0 1 0 1 c c c e إذن lt lt lt lt 1 2 1 t e dt lt لدينا -أ 2 2 2 2 2 2 0 0 0 0 0 2 t t t f t dt t e dt t e dt e dt g 0 g f t dt 0 ب- لدينا x و إذن g قابلة للاشتقاق على ولدينا f دالة متصلة على x g x f t dt 0 لدينا x x g x f t dt f x lt إذن g تزايدية قطعا و أن x 1 0 g x f x ج- نعلم أن g دالة متصلة على المجال 1 1 المجال على ولدينا 1 1 2 2 2 0 0 1 1 1 0 t t g e dt e dt gt لأن 1 2 1 t e dt lt و 0 g f t dt t 0 f t 0 أن وحيث g lt0 فإن lt حسب مبرهنة القيم الوسيطية نستنتج أن المعادلة g x 0 تقبل حلا وحيدا في المجال 1 t 0x و x gt 0ليكن -أ 3 لدينا 2 2 2 2 2 2 2 2 0 0 0 0 0 1 x x x x t x t x t t x x t e e e dt e dt x xe e dt x lt lt lt lt lt lt lt lt lt lt 2 2 1 2 0 1 1 x x t x x x t x e e dt e lt lt lt lt lt lt 0 بما أن 2 lim 1 x x e 0 و lim 1 1 x فإن 0 lim 1 0 x ومنه فإن متصلة على اليمين في x 0 و دالتاهما المشتقتان t 61 و متصلتان وقابلتان للاشتقاق على المجال 2t t e 6 0x ب- ليكنx gt 0 الدالتان t t 6 و 2 حسب تقنية المكاملة بالأجزاء لدينا 6 متصلتان على المجال 2 t t te 0x hhhhhhhhhhhhpKctKcKRKVJ 9 nJ

2 2 2 2 0 0 0 0 1 1 1 2 x x x x t t t t x e dt t e dt te t te dt x x x 2 2 2 2 2 2 0 0 1 x t x x x 2 t x t e dt e t e dt x xe x فإن وبالتالي 2 2 2 2 x x t x x e t e dt x أن بما -ج 2 2 t t t e 6 على متصلة دالة الدالة فإن 2 2 x t x t e dt 6 على للاشتقاق قابلة ولدينا 2 2 2 2 x t x x t e dt x e 2 وبما أن الدالتين x x 6 و ولكل x من فإن الدالة قابلة للاشتقاق على قابلتين للاشتقاق على 2 x x e 6 لدينا 2 2 2 2 2 2 2 2 2 2 2 2 x t x x x t x t x t e dt xe x x e t e dt t e dt x 2 2 2 0 2 2 2 2 2 2 2 2 2 2 x x x t x t t e dt x xe x e x x x t e dt 2 2 وبالتالي فإن 2 0 2 x t x t x e dt x 2 2 وأن د- نعلم أن دالة متصلة على المجال 01 2 0 2 0 x t x x t e dt x إذن تناقصية gt 01 المجال على قطعا 01 1 0 1 1 01 إذن لأن 21 1 e 0 -أ -3 أنظر gt gt 01 01 خلاصة t لدينا 4 أ- ليكن x 0x وليكن 2 2 2 2 3 2 2 2 2 2 2 0 0 0 0 1 3 x x x x t t t t t t e t e t t e dt t dt t e dt 2 2 3 3 x t t e dt x 2 2 ب- لدينا 2 0 2 x t x x t e dt x و 2 3 2 3 x t x x t e dt إذن 3 2 2 01 3 2 2 3 3 x x x x x ليكن -ج x لدينا 2 2 2 2 0 0 0 1 2 0 0 x x x t dt t dt t dt x x e x e x e x x g x وبالتالي فإن x x 0 x g x hhhhhhhhhhhhpKctKcKRKVJ 10 nJ

KhhhhhhhhhhhhhhhhJahhhhhhhhhhhhhhhhhhhhhhhpKctKcKRKVJ 11 nJ المعرفة بما يلي 5 n n u نعتبر المتتالية العددية 0 أ- من أجل n 0 لدينا 2 3 0u0 1 إذن u 0un1 1 أن ونبين 0un 1 أن نفترض n ليكن 9 لدينا 01 01 x x 01 0 1 إذن 0un1 1فإن 0un 1 أن وبما 9 وبالتالي فإنه حسب مبدأ الترجع لدينا n u 0 1 n 01 المجال من x ليكن -ب a b المجال نعتبر على متصلة دالة لدينا b x max و a x min حيث حسب مبرهنة التزايدات المنتهية يوجد على الأقل عدد حقيقي c بحيث وقابلة للاشتقاق على المجال a b المجال a b x c x أي x c x و acb lt lt x c x فإن ومنه إذن g 0 ولدينا فإن 0 1 ltacb ltltlt أن وبما 2 3 على نحصل ثم c 2 3 x c x x إذن 2 01 3 x x x 01 لدينا n ليكن un إذن 2 3 أي u u n n 1 2 3 u u n n 1 ومنه فإن 2 3 nu u n n ولدينا وذلك بعد ضرب طرفي المتفاوتات السابقة على التوالي طرفا بطرف وبعد الاختزال 1 2 3 n n u u un
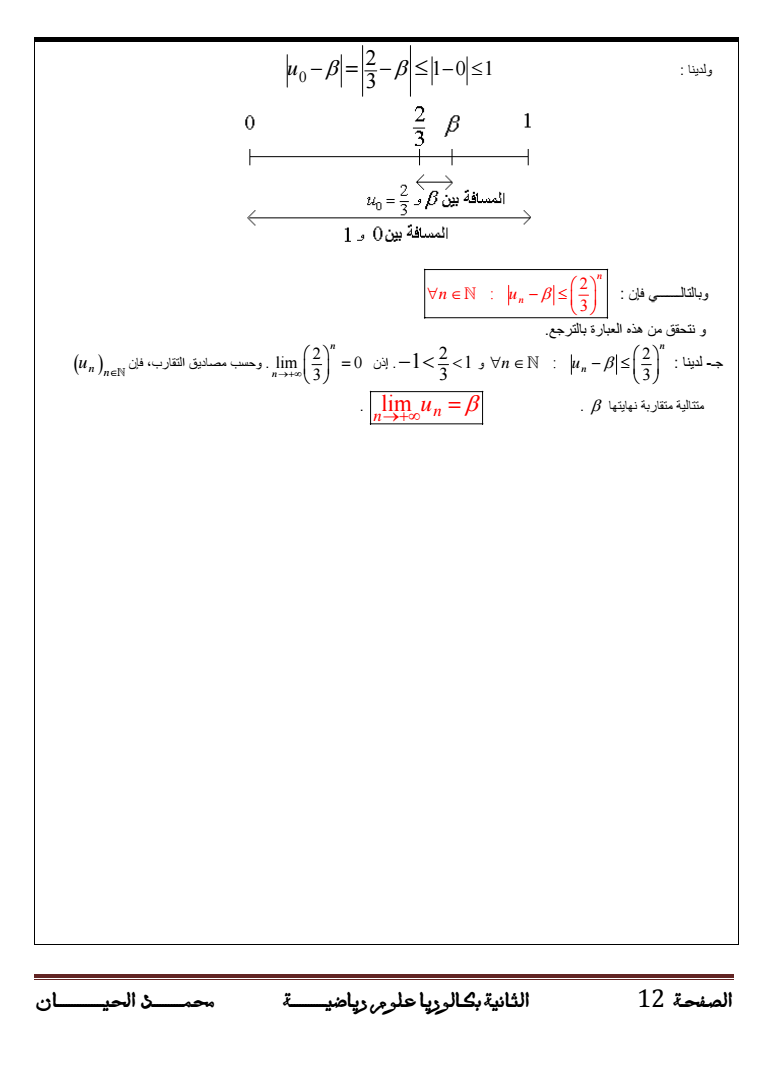
KhhhhhhhhhhhhhhhhJahhhhhhhhhhhhhhhhhhhhhhhpKctKcKRKVJ 12 nJ ولدينا 0 10 1 2 3 u 2 وبالتالي فإن 3 n n un و نتحقق من هذه العبارة بالترجع 2 ج- لدينا 3 n n un و 2 1 3 إذن lt1 lt 2 lim 0 3 n n n u وحسب مصاديق التقارب فإن n lim نهايتها متقاربة متتالية n n u




ثانوية محمد الخامس القنيطرة - تصحيح الامتحان الوطني الموحد الثانية علوم رياضية الأستاذ محمد غريز للباآلوريا أ و ب الدورة - الاستدراآية - 2008 التمرين الأول بالنقطة Mz نقطة آل يربط الذي التطبيق r ليكن - 1 1 1 حيث M z 1 1 3i 3 i z z 2 2 لدينا 1 3i 1 2 و 1 3i 1 2 اذن r دوران مرآزه ذات اللحق 3 i 2 1 3i 1 2 أي 3 i 1 i 3 أي 3 i1 i 3 i 4 و زاويته 2 1 3i arg 2 2 3 بالنقطة Mz النقطة يربط الذي التطبيق h ليكن 2 حيث M z 2 2 z 2 z 3i لدينا -2 ونسبته i مرآزه تحاآي h اذن 2 1 F بالتطبيق Mz صورة هي Mz لتكن - أ 2 Fhor لدينا r h 1 1 M M M z z z 1 لدينا 1 3i 3 i z 2 2 اذن z 2z1 3i و 1 3i 3 i z 2 z 3i 2 2 z i 1 i 3z 3 i أي z 1 i 3z 3 i 3i اذن z i 1 i 3z i أي z i 1 i 3z i 1 i 3 أي و بما أن 4 i 3 1 i 3 2e فإن 4 i 3 z i 2e z i ب لدينا 4 i 3 z i 2e z i zi لدينا zi أجل من اذن هي النقطة الوحيدة التي تحقق F BFA لدينا أ 3 اذن 4 i 3 b i 2e a i أي 4 4 i i 3 3 b 2e a 2ie i و بما أن i 2 i e فان 4 5 i i 3 6 b 2e a 2e i CFB لدينا اذن 4 4 5 i i i 3 3 6 c i 2e 2e a 2e اذن 2 i i 3 6 c 4e a 4e i httpmathkasicima

DFC لدينا اذن 4 2 i i i 33 6 d i 2e 4e 4e أي 3 i i2 2 d 8e a 8e i d 8a 7i منه و d 8a 8i i أي ب لنبين أن النقط وA و D مستقيمية لدينا d i 8a 7i i 8a i ai ai ai اذن d i 8 a i d i بما أن a i عدد حقيقي فان النقط وA و D مستقيمية B 4C 2D1 المتزنة النظمة مرجح أن لنبين ج 4B2C D 0 أي JJJG JJJG JJJG G لدينا 4 52 i ii i 3 63 6 4b i 2c i d i 8e a 8e 8e a 8e 8a 8i 24 5 ii ii 3 3 66 8a1 e e 8e e i 2 2 i i ii i 3 3 33 2 8a1 e e 8e e e i 2 8a1 2cos 8i2cos i 3 3 1 1 8a1 2 82i i 0 2 2 B 4C 2D1 المتزنة النظمة مرجح هو بالتالي و D O u d d - د G 8a 7i 8a 7i 8a a 14i 0 16 Im ai 14i 0 7 Ima 8 7 إذن مجموعة النقط Aa هي المستقيم ذو المعادلة y 8 التمرين الثاني x y x y 3xy 2 x y 1 3x1 3y 1 3x y أن لنبين - أ 1 3x y 1 1 3x1 3y أي 3x y 3x 3y 9xy اذن x y x y 3xy لدينا 3x y 1 1 3x 3y 9xy أي 1 3x1 3y 1 3x y ومنه 1 3x 3y 9xy 1 3x y أي x y x y 3xy y x 3yx yx - ب 2 x y اذن تبادلي xyz xyz 3 x yz اذن تجميعي x x e x x e 3xe x x e1 3x 0 e 0 أو 1 3x 0

ن هو العنصر المحايد للقانون إذن 0 1-3x 0 غير ممكن لكل x من يقبل مماثلا في x 1 3 في x يوجد يعني 13 xx 0 بحيث x x 0 x x 3xx 0 x 1 3x x لان 1 x 3 x x 1 3x بالتالي و 1 3 تبادلية زمرة x 1 3x - أ 2 x y 1 3x y لدينا 1 2 x y 3 1 3x1 3y اذن xy x y أي تشاآل من اذن 1 3 نحو 1 x y x 3 y y x y 1 3x 1 y x 3 لنبين أن 1 x 3 نفترض أن 1 x 3 y 0 آون مع تناقض 1y 1 y 0 3 3 تقابل من إذن 1 3 نحو - ب 1 1 1 3 3 تناقصية لان 1 x 3 gt 1 x 3 x 0 إذن 1 3 1 عنصرا من ليكن y من هل يوجد x 1 3 x y بحيث y x y 1 3x 1 y x 3 1y1 lt اذن lt y 0 ذن لدينا lt y 0 ا أي 1y 1 3 3 أي lt 1 x 3 lt اذن 1 3 2

1 y 3 1 3y من 1 و 2 نستنتج أن 1 3 وبالتالي 1 1 3 ج لدينا 1 1 3 3 و 1 3 لان 1 0 3 1 ليكن x و y عنصران من 3 لدينا y xy x 1 3y اذن y y x 3x 1 3y 1 3y أي x 3xy y 3xy 1 3y أي x y xy 1 3y لدينا 1 x y 1 3y 3x 3y 1 3x 3 1 3y 31 3y 31 3y و بما أن 1 x gt و 3 1 y 3 1 3y 0 gt و 1 3x 0 gt فان lt اذن 1 3x 0 31 3y gt أي xy 1 1 3y 3 lt اذن 1 xy 3 و بالتالي 1 3 للزمرة جزئية زمرة 1 3 لدينا n0 أجل من أ 3 0 و x 0 1 0 x 1 اذن 0 0 x x أن نفترض n n x x أن نبين و n 1 n 1 x x لدينا n 1 n x x x تشاآل لان n x x أي n x x منه و n 1 n 1 x x - ب n 1 n x x n n x x n 1 n x 1 3x n n 1 1 3x x 3 يلي بما على المعرف الداخلي الترآيب قانون T ليكن 4 1 xTy x y 3 2 x y - أ 1 xTy x y 3 2 x y 1 y x 3 xTy yTx إذن T تبادلي

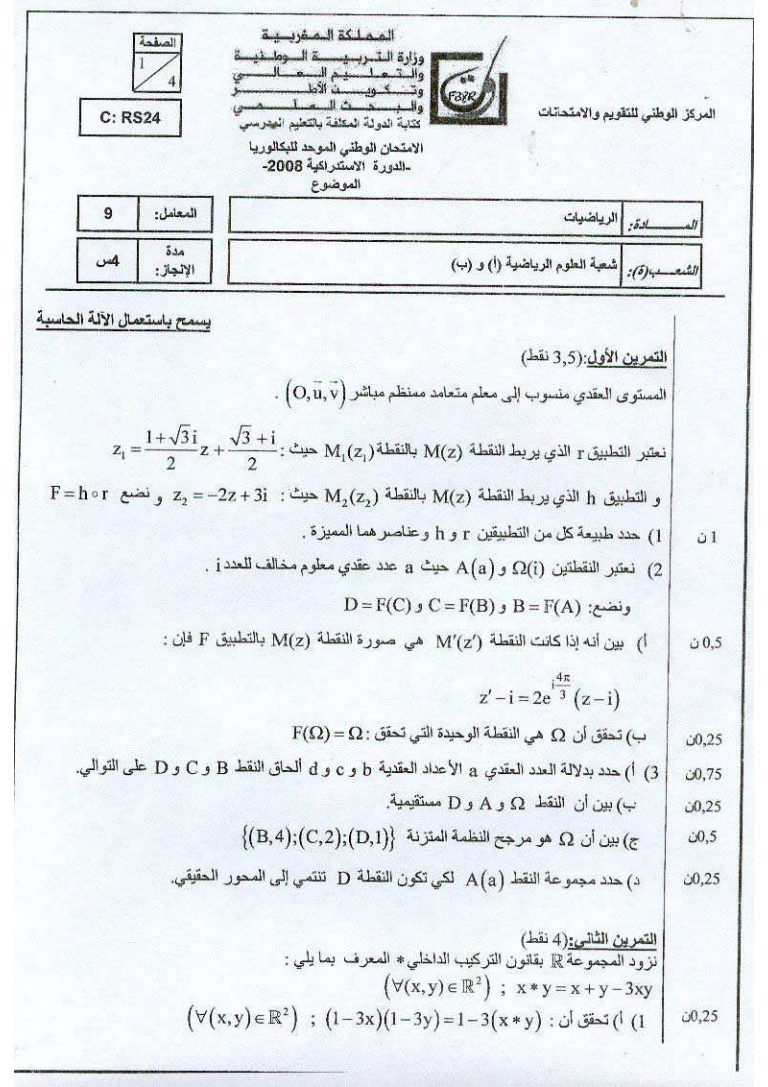
لدينا 1 xTyTz x y Tz 3 3 x yz 2 اذن xyz 3 لدينا 1 xTyTz xTy z 3 2 اذن xyz 3 من x yz لكل xTyTz xTyTz اذن 3 اذن T تجميعي لدينا 1 11 xT x x 3 33 x 1 اذن هو العنصر المحايد للقانون 3 T x يقبل مماثلا في T يعني يوجد x في E بحيث 1 xTx هذه العلاقة آافية لان T تبادلي 3 1 11 xTx x x 3 33 2 x x 3 اذن آل عنصر من له مماثل في T و بالتالي T زمرة تبادلية ب لدينا T زمرة تبادلية و 1 3 تبادلية زمرة لنبين أن توزيعي بالنسبة للقانون T x yTz x yTx z أي 3 تبادلي لان آافية العلاقة هذه x yz لدينا 1 x yTz x y z 3 اذن 1 1 x y z 3xy z 3 3 اذن 1 x yTz 2x y z 3xy 3xz 3 1 x yTx z x y 3xyTx z 3xz لدينا اذن 1 x yTx z x y 3xy x z 3xz 3 1 x yTx z 2x y z 3xy 3xz 3 2 من 1 و 2 نستنتج أن توزيعي بالنسبة للقانون T و بالتالي T جسم تبادلي لدينا آرة بيضاء و ثلاث آرات حمراء التمرين الثالث نسحب عشوائيا آرة من الصندوق نسجل لونها ثم نعيدها الى الصندوق X رتبة السحبة التي توققت فيها التجربة X2 1 يعني سحب آرتين بيضاوتين أو آرتين حمراوين أي BB أو RR اذن 11 33 pX 2 44 44
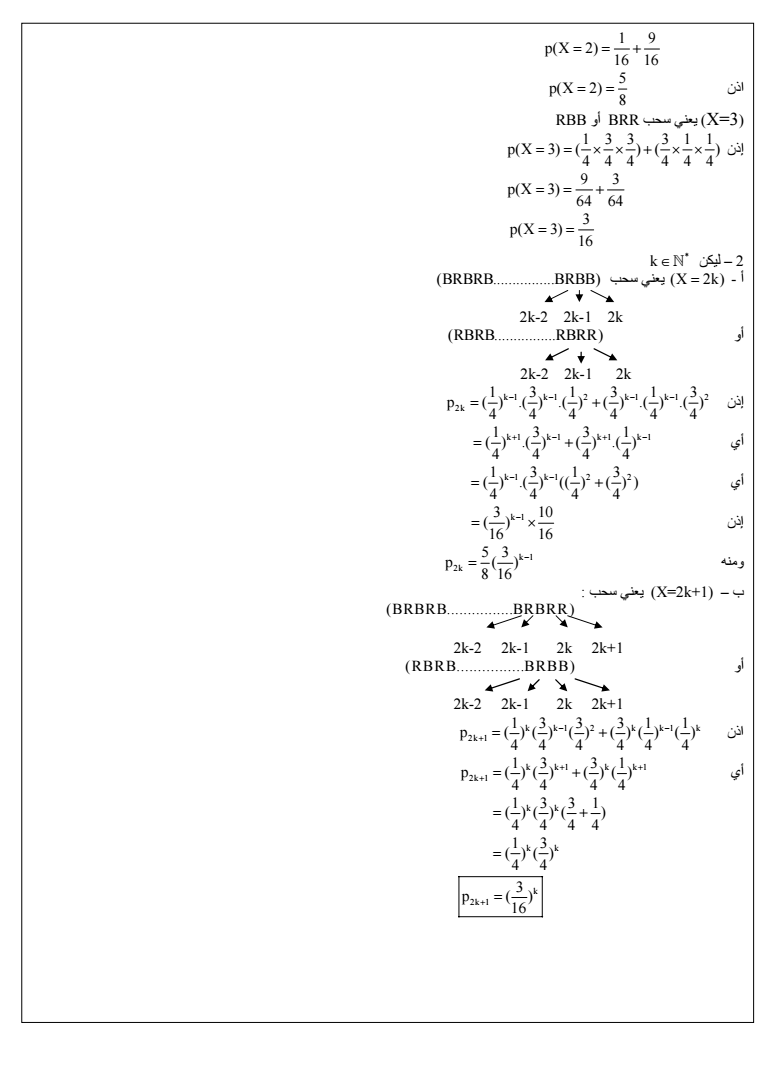
1 9 pX 2 16 16 اذن 5 pX 2 8 RBB أو BRR سحب يعني X3 إذن 133 311 pX 3 444 444 9 3 pX 3 64 64 3 pX 3 16 ليكن 2 k BRBRBBRBB سحب يعني X 2k - أ 2k-2 2k-1 2k RBRBRBRR أو 2k-2 2k-1 2k إذن k1 k1 2 k1 k1 2 2k 131313 p 444444 أي 13 31 k1 k1 k1 k1 44 44 أي 1313 k1 k1 2 2 4444 إذن 3 10 k 1 16 16 ومنه k 1 2k 5 3 p 8 16 ب X2k1 يعني سحب BRBRBBRBRR 2k-2 2k-1 2k 2k1 RBRBBRBB أو 2k-2 2k-1 2k 2k1 اذن k k1 2 k k1 k 2k 1 13 3 31 1 p 44 4 44 4 أي k k1 k k1 2k 1 13 31 p 44 44 1 3 31 k k 4 4 44 1 3 k k 4 4 k 2k 1 3 p 16

التمرين الرابع 1 I 2 لتكن f الدالة المعرفة على يلي بما ln1 2x fx x 0 x f 0 2 - 1 x0 x0 ln1 2x lim f x lim 2 2x 1 2 2 f 0 في متصلة f إذن 0 x 0 - 2 1 a 2 a 0 2 2 أ لتكن a h x ln1 2a 2ax ln1 2x 2xa لدينا a h a 0 a و h 0 0 h متصلة على المجال المغلوق الذي طرفاه 0 و a a و ق ش على المجال المفتوح الذي طرفاه 0 و a a h b 0 اذن حسب مبرهنة رول Rolle يوجد عدد حقيقي b محصور بين 0 و a بحيث 2 لدينا a 2 h x 2ln1 2a 2ax 2a 1 2x 2 a 1 h b 0 ln1 2a 2ab 1a 1 2b 2 ln1 2a 2a 2b a b1 2b 2 ln1 2a 2a 2 a 1 2b ب - 2 x0 x0 f x f 0 ln1 2x 2x lim lim x x 2 حسب س - أ - ln1 2x 2x 2 x 1 2b بحيث b محصور بين 0 و x اذا آان lt x 0 فان gt gt 0bx إذن 2 x0 b0 ln1 2x 2x 2 lim lim 2 x 1 2b d f 0 2 اذن f ق ش على يمين 0 و اذا آان gt x 0 فان gt gt xb0 اذن x0 b0 f x f 0 2 lim lim 2 x 1 2b g f 0 2 اذن f ق ش على يسار 0 و و بالتالي f ق ش في 0 و f 0 2 3 أ الدالة f ق ش على I 0 لأنها مرآب و خارج دالتين ق ش على I 0 2 لدينا 2 x ln1 2x 1 2x f x x x I 0 2 اذن 2x 1 2xln1 2x f x x 1 2x 2 أي gx f x x 1 2x gx 2x 1 2xln1 2x بحيث
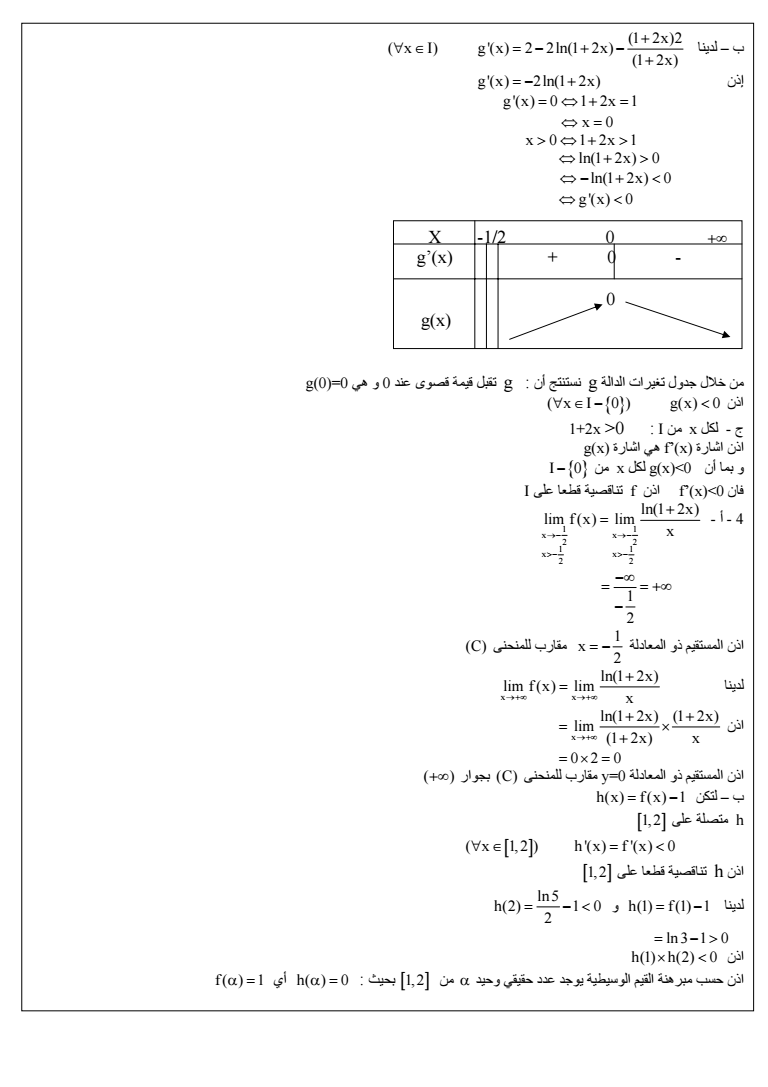
لدينا ب 1 2x2 g x 2 2ln1 2x 1 2x x I g x 2ln1 2x إذن g x 0 1 2x 1 x 0 x 0 1 2x 1 gt gt gt ln1 2x 0 lt ln1 2x 0 lt g x 0 من خلال جدول تغيرات الدالة g نستنتج أن g تقبل قيمة قصوى عند 0 و هي g00 x I 0 gx 0 lt اذن 12x gt0 I من x لكل - ج اذن اشارة fx هي اشارة gx I 0 من x لكل gxlt0 أن بما و فان fxlt0 اذن f تناقصية قطعا على I 4 - أ - 1 1 x x 2 2 1 1 x x 2 2 ln1 2x lim f x lim x gt gt 1 2 1 اذن المستقيم ذو المعادلة x مقارب للمنحنى 2 C لدينا x x ln1 2x lim f x lim x x اذن ln1 2x 1 2x lim 1 2x x 02 0 اذن المستقيم ذو المعادلة y0 مقارب للمنحنى C بجوار hx fx 1 لتكن ب 1 2 على متصلة h x 1 2 h x f x 0 lt اذن h تناقصية قطعا على 1 2 و h1 f 1 1 لدينا ln 5 h2 1 0 2 lt ln 3 1 0 gt h1 h2 0 lt اذن اذن حسب مبرهنة القيم الوسيطية يوجد عدد حقيقي وحيد من 1 2 بحيث h 0 أي f 1 X -12 0 gx 0 - gx
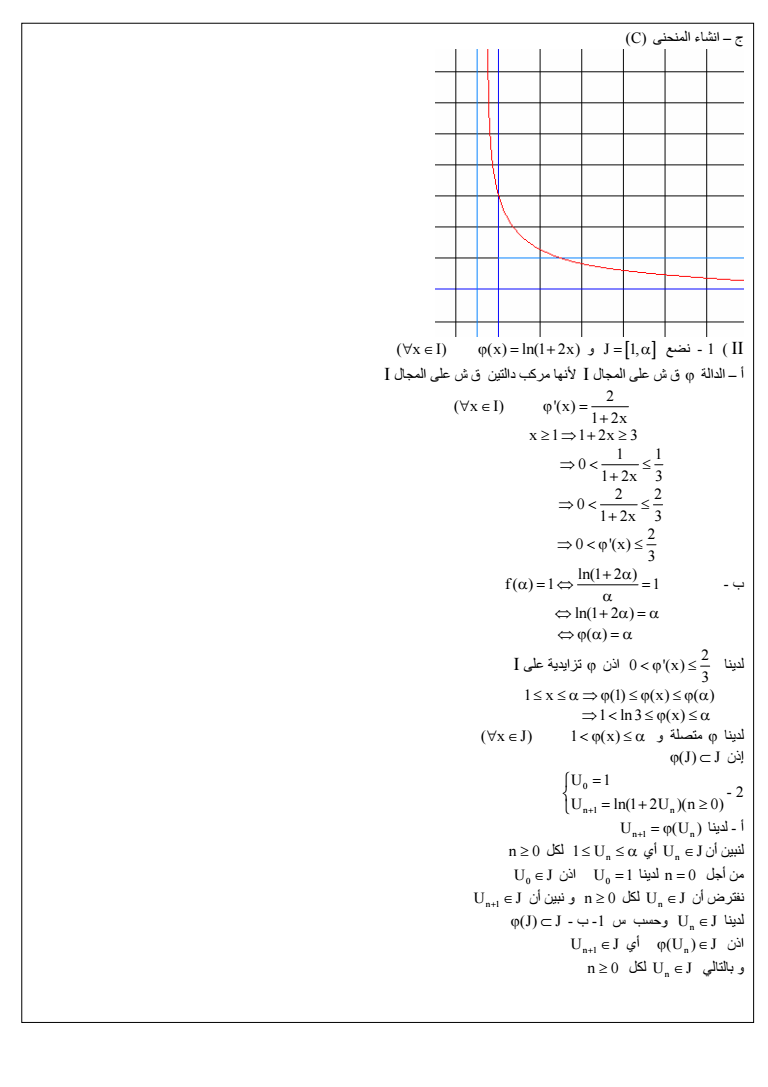
ج انشاء المنحنى C x I x ln1 2x و J 1 نضع - 1 II أ الدالة ق ش على المجال I لأنها مرآب دالتين ق ش على المجال I 2 x 1 2x x I x 1 1 2x 3 1 1 0 1 2x 3 lt 2 2 0 1 2x 3 lt 2 0 x 3 lt - ب ln1 2 f 1 1 ln1 2 لدينا 2 0 x 3 I على تزايدية اذن lt 1 x 1 x lt 1 ln 3 x x J 1 x lt و متصلة لدينا J J إذن - 2 0 n1 n U 1 U ln1 2U n 0 لدينا - أ U U n1 n أن لنبين n 0 لكل 1 U n أي U J n لدينا n 0 أجل من U J 0 اذن U 1 0 أن نفترض U J n 1 أن نبين و n 0 لكل U J n لدينا J J - ب -1 س وحسب U J n اذن n U J n 1 أي U J بالتالي و n 0 لكل U J n

1 2 لدينا ب 11 01 lt أي 2 1 اذن 0 اذن 2 U 3 n نفترض أن n 2 U 3 n 0 لكل و نبين أن n 1 n 1 2 U 3 Un و ق ش على المجال المفتوح الذي طرفاه و Un لدينا متصلة على المجال المغلوق الذي طرفاه و Un بحيث اذن حسب مبرهنة التزايدات المنتهية يوجد c محصور بين و n n U c U و بما أن 2 0 x 3 فان x 1 لكل lt 2 c 3 لدينا و U U n1 n و حسب س 1 ب - اذن n1 n 2 U U 3 n حسب افتراض الترجع لدينا n 2 U 3 اذن n 1 n 1 2 U 3 n و بالتالي n 2 U 3 n 0 لكل ج المتتالية 2 n 3 لان 0 نهايتها و متقاربة 2 1 1 3 lt lt U n n متقاربة و n اذن حسب مصاديق التقارب المتتالية lim U III x لتكن F الدالة المعرفة على I بما يلي Fx f tdt 1 - أ f متصلة على I اذن تقبل دالة أصلية على I x I x f x و I على ش ق بحيث x لدينا 0 Fx t x 0 اذن F ق ش على I لانها مجموع دالتين ق ش على I x I Fx x Fx f x ب من خلال مبيان الدالة f نستنتج أن x I fxgt0 اذن Fxgt0 اذن F تزايدية قطعا على I 2 أ لدينا x Fx f tdt اذن 1 x 0 1 Fx f tdt f tdt x 1 x 1 Fx f tdt

x 1 ln1 2t Fx dt t 1 1 ln1 2t ln1 2t t 1 2t t 1 2t t 1 2t x x 1 1 ln1 2t ln1 2t dt dt t 1 2t و بما أن x 1 ln1 2t Fx dt t فان x 1 ln1 2t Fx dt 1 2t ب لدينا x x 1 1 ln1 2t 1 dt ln1 2t ln1 2tdt 1 2t 2 اذن x x 2 1 1 ln1 2t 1 dt ln1 2t 1 2t 4 أي 1 1 2 2 ln1 2x ln 3 4 4 اذن 1 1 2 2 Fx ln1 2x ln 3 4 4 و بما أن 2 2 x 1 1 lim ln1 2x ln 3 4 4 x فان lim Fx 3 1 نفترض أن الدالة F تقبل نهاية منتهية A على اليمين في 2 1 اذن F تقبل تمديدا بالاتصال على اليمين في 2 1 الدالة المعرفة على أ لتكن F 2 بما يلي Fx Fx x I 1 F 2 A F هي التمديد بالاتصال للدالة F على اليمين في 1 2 1 متصلة على لدينا F x 2 و ق ش على 1 x 2 اذن حسب مبرهنة التزايدات المنتهية TAF 1 Fx F 1 2 c x Fc 2 1 x 2

اذن 1 Fx Fcx 2 A 1 Fx f cx 2 A لدينا 1 c x 2 lt lt f c f x فان I على تناقصية بما أن f و اذن 1 Fx f xx 2 A - ب 1 1 x x 2 2 1 1 x x 2 2 1 Fx F Fx 2 lim lim 1 1 x x 2 2 gt gt A 1 x 2 1 x 2 lim f x gt بما أن و 1 x 2 1 x 2 lim f x gt فان 1 x 2 1 x 2 1 Fx F 2 lim 1 x 2 gt الدالة F اذن غير ق ش على اليمين في 12 ياسر غريز بعثه





الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 1 - تصحيح موضوع الدورة العادية 18 2007 الأستاذ الحيان تصحيح الامتحان الوطني الموحد للبكالوريا الدورة العادية 2007 الثانية بكالوريا علوم رياضية الرياضيات التمرين الأول ليكن I 1 2 E لدينا 2 a b E a b a b ab 2 ليكن -أ 1 2 لدينا ab E 11 11 21 21 2 1 2 2 2 22 22 a b ab a b a b ab a b ab E لدينا 2 ب- ليكن 1 210 2 إذن bE b 210 و aE a a 0 فإن ومنه a b 21 21 0 1 1 21 21 2 2 أي a b a b 1 2 a b فإن وبالتالي a b E فإن ومنه 2 ab E a b E إذن قانون ترآيب داخلي في E 2 لدينا قانون ترآيب داخلي في E وبما أن الجمع والضرب قانونين تبادليين وتجميعيين في فإن قانون تبادلي وتجميعي في E E في ل بالنسبة المحايد العنصر هو 0 إذن aE a a aa 0 0 لدينا ليكن 2 لدينا ab E 1 1 0 21 21 0 2 2 21 21 1 1 2 1 2 2 1 1 2 1 2 1 2 2 1 2 1 ab a b a b b a b a a b a a b a b a أن وبما 1 1 2 21 0 1 2 21 2 a b aa وهذا غير ممكن فإن a b E 2 1 وبالتالي فإن لكل a E مماثل وحيد a b a في E بالنسبة للقانون وبالتالي فإن E زمرة تبادلية M حلقة واحدية وحدتها II 2 نعلم أن 1 0 0 1 I M فضاء متجهي حقيقي 2 وأن M2 1 2 التي تكتب على شكل F مجموعة المصفوفات من 2 2 a a a a a M a E حيث

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 2 - تصحيح موضوع الدورة العادية 18 2007 نضع 1 1 1 1 A لدينا -أ 1 2 11 11 2 2 11 2 2 1 1 1 1 22 1 1 A A 2 A 2A ولدينا 10 1 1 1 2 2 22 01 1 1 2 a a a a I A Ma a a 2 a M aI A ليكن -ب 2 لدينا ab E 2 2 2 22 2 a b ab a b M a Mb I A I A A A A I 2 2 2 2 22 a b a b a b ab M a M b I A I A abA A A A I I 2 a b M a Mb A a b I M ب1I السؤال حسب a b E و M a Mb a b M إذن من مستقر جزء F إذن Ma Mb Ma b F فإن ومنه 2 M 2 نعتبر التطبيق E a a Ma 6 F ليكن -أ 2 a b Ma b Ma Mb a b لدينا ab E إذن تشاآل من E نحو F aE B a إذن a E B Ma إذن B F ليكن وعليه فإن شمولي من E نحو F ولدينا 2 2 22 a b ab a b Ma Mb I A I A A A a b إذن تبايني من E نحو F وبالتالي فإن تشاآل تقابلي من E نحو F ب- بما أن تشاآل تقابلي من E نحو F و E زمرة تبادلية فإن F زمرة تبادلية التمرين 2 a ii ليكن المعادلة في نعتبر -أ 1 I 2 2 لدينا u ai ليكن E 11 1 0 z a iz a i 2 22 2 2 2 2 22 2 2 2 11 1 11 1 2 11 1 21 1 1 11 1 0 u a iu a i a i a i a i a i a ai a a i ai i a i a ai a i ai a ai a i i a i u a iu a i إذن u ai حل للمعادلة E

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 3 - تصحيح موضوع الدورة العادية 18 2007 ب- ليكن v الحل الآخر للمعادلة E لدينا 11 11 1 1 1 1 b uv a i v a i u a v a i ai v i a ai a i v ai إذن a 1 أن نفترض 2 2 فإن ومنه aa a 1 1 a a أ- بما أن 1 1 1 1 1 1 1 i u u a i a i ai a i u i ai a v a i ai v v ai i ai ia i a u فإن v لدينا -ب 2 22 2 a a a i a aa ai a ai a i u 2 2 12 2 u aaa i 2 ج- لدينا 2 arg 2arg 2 u u لدينا و 2 arg arg u aaa i 2 2 arg arg a aa i 2 2 ولدينا a a i i m i ma i I I 22 22 1 a I I I I ma a ma ma ma 1 1 1 0 12 ولدينا ومنه فإن 2 a a i ma 22 1 2 2 إذن I 2 arg aa i فإن وعليه 2 2 2 arg arg u a 2 أي 2 2arg arg u a 1 وبالتالي فإن 2 4 arg arg u a 1 طريقة 3 u iv 2 2 i فإن ومنه u iv a i i ai i 1 2 و u v u iv u iv لدينا u v 2 فإن وبالتالي طريقة 2 لدينا a 1 إذن aa 1 ومنه فإن u v a i ai a i aa ai a i a a i a i a i a i a i 1 ai ai aa i a i 2 2 22 Re i ea R ولدينا 2 إذن ai ai a i a 2 21 R R e e وبما أن

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 4 - تصحيح موضوع الدورة العادية 18 2007 2 2 2 1 1 1 0 1 11 2 1 1 ea a ea e a e a e a e a R R R R R R 2 2 2 1 2 ea a e a ai ai R R أن نستنتج ومنه ai ai 2 و u v ai ai إذن u v 2 II 1 2 Oe e المستوى العقدي P منسوب إلى معلم متعامد ممنظم JJG JJG m 2 ليكن نعتبر E m مجموعة النقط M a من المستوى العقدي P بحيث uv m u v ai ai أن نعلم 1 لتكن F i و Fi نقطتين من المستوى العقدي P اللتان لحقاهما على التوالي i و i u v m a i a i m MF MF m لدينا 2 2 البؤرية المسافة أن وبما F F FF z z i i i فإن muv 2و أي O أصل المعلم m c 2b 2 إذن E m إهليلج مرآزه منتصف القطعة FF حيث a x iy نضع 2 2 x y أ- لدينا M uv m a E m MF MF m M x y و F0 1 و F 01 أن نعلم MFx y 1 إذن JJJJJJG MFx y 1 و JJJJJJG فإن ومنه 2 2 22 22 MF x y MF x y 1 1 إذن 2 2 MF MF MF MF y 4 ومنه MF MF y 4 MF MF m أن وبما m MF MF y 4 فإن أي 4 MF MF y m

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 5 - تصحيح موضوع الدورة العادية 18 2007 وعليه فإننا نجد 4 4 2 y m MF MF m MF MF MF my m 2 إذن 2 m MF y m ومنه فإن 2 2 2 2 2 2 4 2 4 2 m y m MFy y m m أن بما و 2 2 2 فإن MFx y 1 2 2 2 2 2 2 1 4 4 x y m y y m أي 2 2 2 2 2 2 12 4 4 x m y yy y m يكافئ 2 2 2 2 2 1 4 4 x m y y m 2 وبالتالي فإن معادلة ديكارتية للإهليلج E m هي 2 2 2 1 1 4 4 x m y m بطريقة أخرى Oi j نعلم أن معادلة ديكارتية للإهليلج E m في المعلم JJG JJG تكتب على شكل 2 2 2 2 1 x y a b أي 2 22 2 2 x y a b a 2 و 2 m و bm b 2 1 2 2 FF c إذن 2 2 2 2 2 22 2 2 1 1 2 4 m m cb abc a 2 وبالتالي فإن ديكارتية للإهليلج E m هي 2 2 2 1 1 4 4 x m y m 2 2 ب- لدينا 4 3 3 4 إذن E xy 2 4 2 2 2 3 1 2 x y E فإن ومنه b 2 و a 3 إذن 2 22 2 c ba 2 31 E إهليلج 4 ومنه فإن - مرآزه O B 0 2 و B 02 و A 30 و A 30 رؤوسه - F0 1 و F 01 بؤرتيه - 1 - تباعده المرآزي 2 c e b
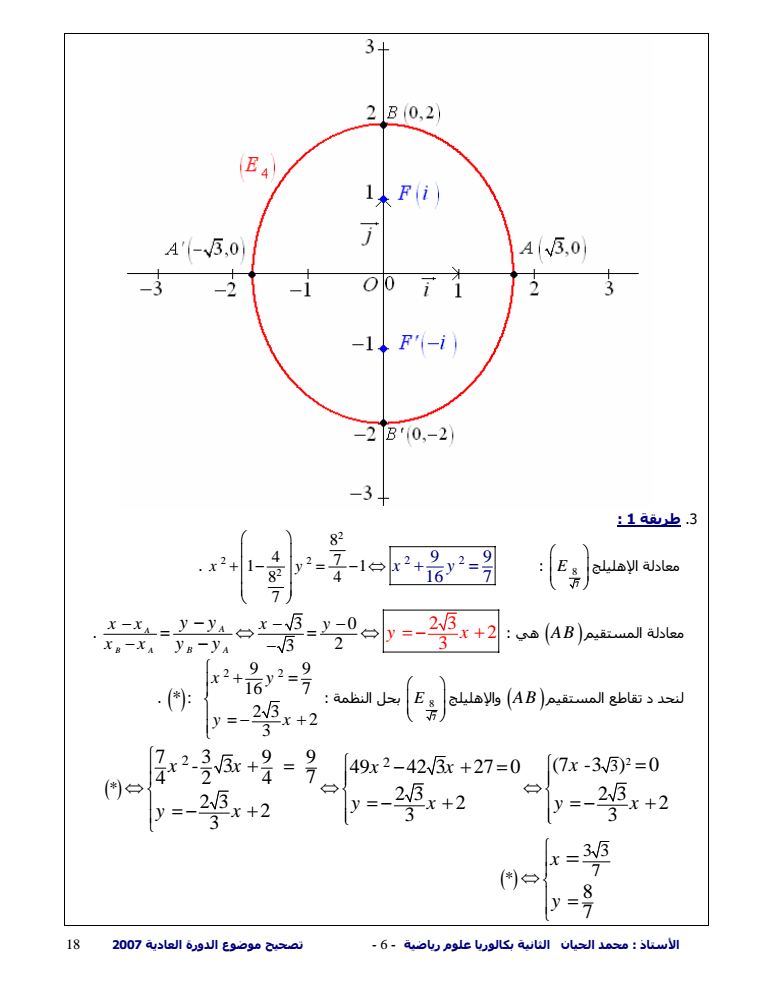
الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 6 - تصحيح موضوع الدورة العادية 18 2007 1 طريقة 3 معادلة الإهليلج 7 E 8 2 2 2 2 2 2 8 4 7 1 1 8 4 7 9 9 16 7 x y x y 3 0 معادلة المستقيم AB هي 3 2 2 3 2 3 A B A A B A x x x y x x y y y y y x لنحد د تقاطع المستقيم AB والإهليلج 7 E 8 بحل النظمة 2 2 9 9 16 7 2 3 2 3 x y y x 2 2 2 3 73 99 -3 49 42 3 27 0 7 -3 0 42 4 7 2 3 2 3 2 3 2 2 2 3 3 3 x x x x x y x y x y x 3 3 7 8 7 x y

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 7 - تصحيح موضوع الدورة العادية 18 2007 ومنه فإن المستقيم AB والإهليلج 7 E 8 338 7 7 يتقاطعان وفق النقطة نعلم أن معادلة المماس للإهليلج 7 2 2 8 9 9 16 7 E x y في النقطة هي 0 0 33 8 7 7 9 9 99 16 16 7 7 399 3 7 7 14 2 3 23 xy x y x y x y x y وبالتالي فإن المستقيم AB مماس للإهليلج 7 E 8 النقطة في 338 7 7 طريقة 2 معادلة الإهليلج 7 E 8 2 2 2 22 2 2 8 4 99 7 1 1 8 4 16 7 7 16 16 7 9 x y xy y x 3737 2 7 7 نعتبر الدالة العددية g المعرفة بما يلي 16 16 7 9 x gx x هي AB معادلة 3 0 3 2 2 3 2 3 x y y x AB مماس للإهليلج 7 E 8 3737 7 7 إذا وجد عدد حقيقي x بحيث 2 3 3 g x أو 2 3 3 g x لدينا 2 16 9 16 19 7 9 x g x x و 3 3 7 2 3 3 ومنه g x x 33 8 7 7 y g لدينا 7 8 338 7 7 E ولدينا معادلة المماس للإهليلج 7 E 8 في النقطة تححدد بما يلي 33 9 8 9 9 23 33 9 2 7 16 7 7 2 3 x y xy y x وهي المعادلة المختصرة للمستقيم AB وبالتالي فإن AB مماس للإهليلج 7 E 8
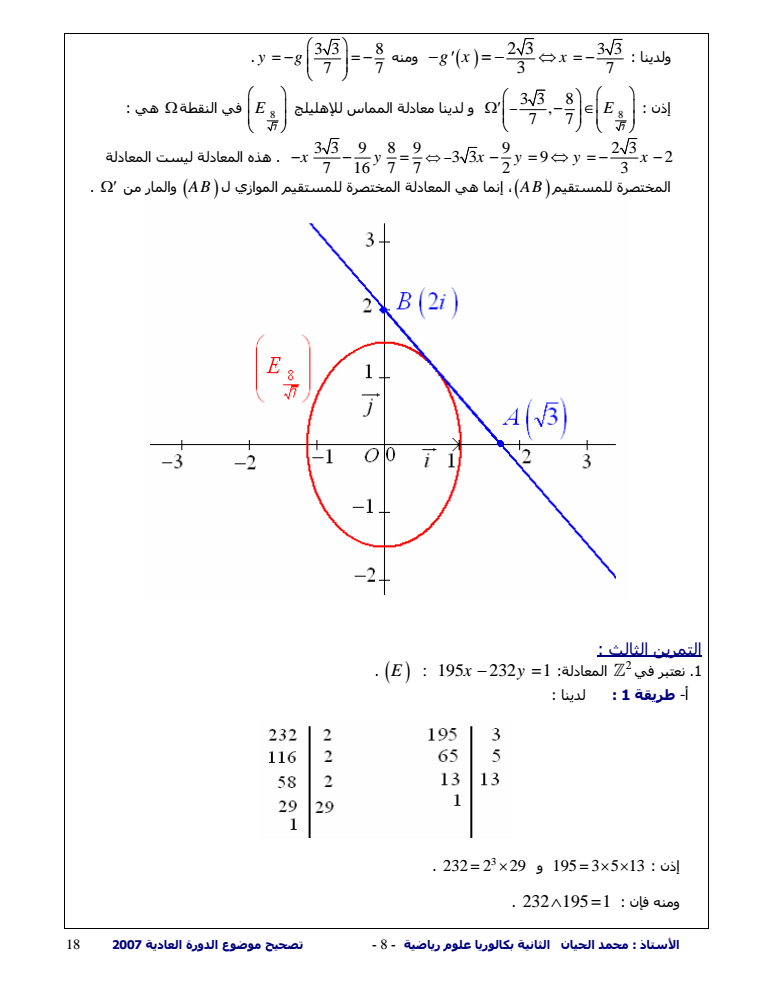
الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 8 - تصحيح موضوع الدورة العادية 18 2007 ولدينا 3 3 7 2 3 3 ومنه g x x 33 8 7 7 y g إذن 7 8 33 8 7 7 E و لدينا معادلة المماس للإهليلج 7 E 8 في النقطة هي 33 9 8 9 9 23 33 9 2 7 16 7 7 2 3 المعادلة ليست المعادلة هذه x y xy y x المختصرة للمستقيم AB إنما هي المعادلة المختصرة للمستقيم الموازي ل AB والمار من التمرين الثالث في نعتبر 1 2 E 195 232 1 x y المعادلة أ- طريقة 1 لدينا و 195 3 5 13 إذن 3 232 2 29 232 195 1 فإن ومنه

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 9 - تصحيح موضوع الدورة العادية 18 2007 طريقة 2 حسب تقنية القسمة الأقليدية المتتابعة لأقليدس لدينا ومنه نستنتج أن 232 195 1 بالإظافة إلى معاملي Bezout ب- لدينا 232 195 69 232 69 إذن Gauss hx h 69 232 فإن ومنه x x أي hx h 69 232 نعوض هذا التعبير في العلاقة فنجد 195 232 232 58 58 hy y 195h y h 58 195 أي h حيث x 69 232 58 195 y hh فإن ومنه x y 69 232 232 58 195 195 h h 1 1 و k نجد k h 1 وبوضع x y 163 232 137 195 h h 1 1 يكافئ k حيث x y 163 232 137 195 k k وبما أن الأزواج 163 232 137 195 k k حيث k تحقق المعادلة E فإن مجموعة S 163 232 137 195 k k k هي E المعادلة حلول 195 1 232 d و 0 232 d بحيث طبيعيا صحيحا عددا d ليكن -ج لدينا ب1 السؤال حسب m dm 195 232 1 لدينا k k d 163 232 إذن k kk d m 163 232 137 195
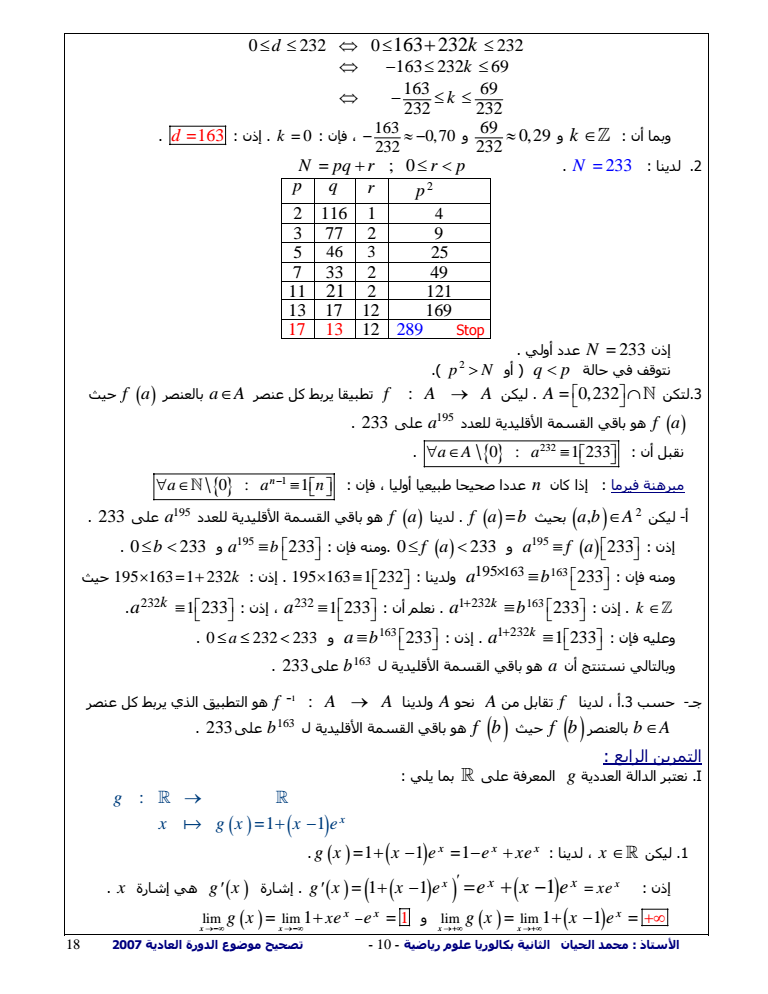
الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 10 - تصحيح موضوع الدورة العادية 18 2007 0 232 0 232 163 232 69 163 69 232 232 d 163 232 k k k و k أن وبما 69 029 232 و 163 070 232 d 163 إذن k 0 فإن N pq r r p lt 0 N 233 لدينا 2 2 r p p q 2 116 1 4 3 77 2 9 5 46 3 25 7 33 2 49 11 21 2 121 13 17 12 169 17 13 12 289 Stop إذن N 233 عدد أولي أو q p lt حالة في نتوقف 2 p gt N A 0232 لتكن3 حيث f a بالعنصر a A عنصر آل يربط تطبيقا f A A ليكن a على f a 195 233 هو باقي القسمة الأقليدية للعدد أن نقبل 232 aA a 0 1 233 1 0 1 n a an مبرهنة فيرما إذا آان n عددا صحيحا طبيعيا أوليا فإن ليكن -أ 2 للعدد الأقليدية القسمة باقي هو f a لدينا f a b بحيث ab A 195 233 على a إذن 195 a fa 233 فإن ومنه 0 233 f a lt و 195 a b 233 0 233 lt b و فإن ومنه 195 163 163 a b 233 195 163 1 232 ولدينا حيث 195 163 1 232 k إذن إذن k 1 232 163 233 k a b أن نعلم 232 a 1233 إذن 232 1 233 k a فإن وعليه 1 232 1 233 k a إذن 163 a b 233 0 232 233 lt a و b على163 233 وبالتالي نستنتج أن a هو باقي القسمة الأقليدية ل هو التطبيق الذي يربط آل عنصر 1 f A A ج- حسب 3أ لدينا f تقابل من A نحو A ولدينا ل الأقليدية القسمة باقي هو f b حيث f b بالعنصر b A 163 233على b التمرين الرابع I نعتبر الدالة العددية g المعرفة على بما يلي 1 1 x g x gx x e 6 1 11 لدينا x ليكن 1 x x x g x x e e xe 1 1 1 إذن x x x x gx x e e xe xe x إشارة هي g x إشارة lim lim 1 1 x x x gx x e lim lim 1 1 و x x x x gx e e x

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 11 - تصحيح موضوع الدورة العادية 18 2007 0 قيمة دنيا مطلقة للدالة g على إذن x gx 0 ولدينا g 0 0 لدينا 2 0 على قطعا تناقصية g x gx g gx lt gt gt 0 00 إذن 0 على قطعا تزايدية g x gx g gx gt gt gt 0 00 إذن فإن وبالتالي gt x gx 0 II لتكن f الدالة العددية المعرفة على بما يلي 0 1 0 1 x x fx x e f 1 1 lim lim lim 1 0 1 1 x x xx x x x x f x e e e lim 0 لأن x x x e 0 و 1 lim x x e 0 lim lim 1 1 01 lim 0 x x x x x x x xe f x e e x x lim 0 لأن x x xe lim 0و x x e 2 00 0 1 1 1 lim lim lim 0 1 x x xx x e x x fx f e لأن 0 1 lim 1 x x e x إذن f متصلة في 0 x لدينا 3 أ- ليكن 2 2 22 1 1 1 1 1 1 11 1 1 x x x x x xx x x x e xe x x x g x f x e e e ee e xe e هي إشارة g x ومنه نستنتج جدول تغيرات الدالة f على ب- إشارة f x على lim lim 1 x x x x f x e lim 0 لأن x x e

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 12 - تصحيح موضوع الدورة العادية 18 2007 4 ليكن x لدينا x t J x te dt أ- نضع t ut e vt t إذن 1 t ut e v t لدينا u و v متصلتان وقابلتان للاشتقاق على حسب تقنية المكاملة بالأجزاء لدينا 0 0 0 0 x x x x t J x te dt u t v t dt u t v t u t v t dt 0 0 0 0 1 x x x t t x t xx J x te e xe e xe e dt 1 فإن وبالتالي x x Jx e e x 0 ب- ليكن x لدينا x t J x te dt x آان إذا 0 01 t x x t e e te te t x t xt فإن إذن 2 22 2 0 00 0 0 2 22 2 x x x xx x t x t tx x x te te t dt dt dt e J x J x e ومنه فإن 2 2 2 2 2 2 x x xx x x e Jx e x آان إذا t 0 لأن x t t x e e te te t 00 1 tx x t فإن إذن 0 0 2 22 2 0 00 2 22 2 x x xx x x x t t tx x x te te t dt dt dt e J x J x e وعليه فإن 2 2 2 2 x x x J x e فإن ومنه 2 2 2 2 2 2 x x xx x x e Jx e هذه العلاقة تظل صحيحة من أجل x 0 وبالتالي فإن 2 2 2 2 2 2 x x xx x x x e Jx e ليكن -ج 1 لدينا x x x J xee x و 2 2 2 2 2 2 x x xx x x e Jx e إذن 2 2 2 2 1 2 2 x x x x xx ee x x x e e 2 ومنه 2 2 1 1 1 2 2 x x x x x xx e x e e x e e 2 وبالتالي فإن 2 2 1 1 1 2 2 x x x xx e x x xe e

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 13 - تصحيح موضوع الدورة العادية 18 2007 2 د- لدينا 2 2 1 1 1 2 2 x x x xx e x x xe e و 2 1 1 lim 2 2 x x x e 2 و 0 1 1 lim 2 2 x x x e 0 2 حسب خاصيات الترتيب والنهايات لدينا 1 1 lim 2 x x e x x ومنه فإن 2 0 00 0 1 0 1 1 1 lim lim lim l 0 1 im 1 1 2 1 x x x x x xx x x x fx f e x e x x x e x e x e x ولدينا 0 في للاشتقاق قابلة f إذن 1 0 2 f x لدينا 5 أ- ليكن 2 2 4 2 2 4 1 1 1 12 1 1 1 x x x xx x x x x g x e gx e e g x xe e e g x e f x e e 2 4 3 12 1 1 2 1 1 xx x x x x x x xe e e g x e e f x xe gx e e 3 22 1 1 x x x x e f x xe x x e e 3 2 2 1 x x x x e f xe x e 2 2 نضع x ليكن -ب x لدينا hx e x x 2 2 2 1 1 1 0 x xx x hx e x x e e x e x g x إذن h تزايدية على وبما أن h 0 0 فإن 0 0 x hx h h x و 0 0 x hx h h x ج- لدينا 2 1 1 x x x e h x x fx e e هي إشارة إشارة f x على 1 x h x e x لدينا ليكن
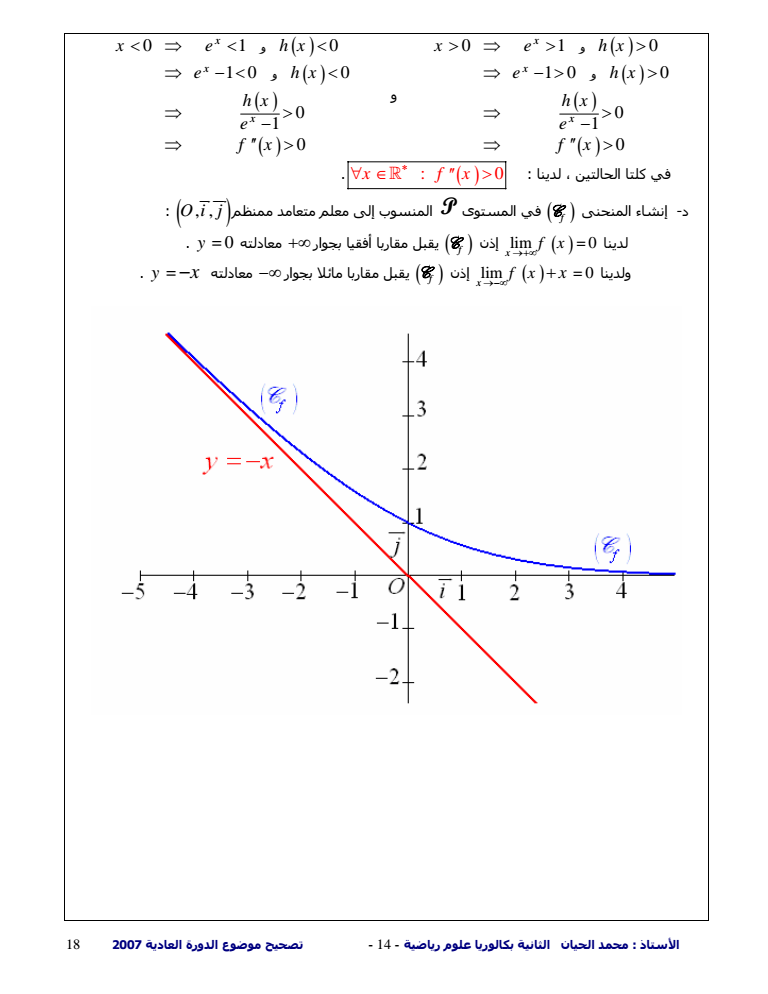
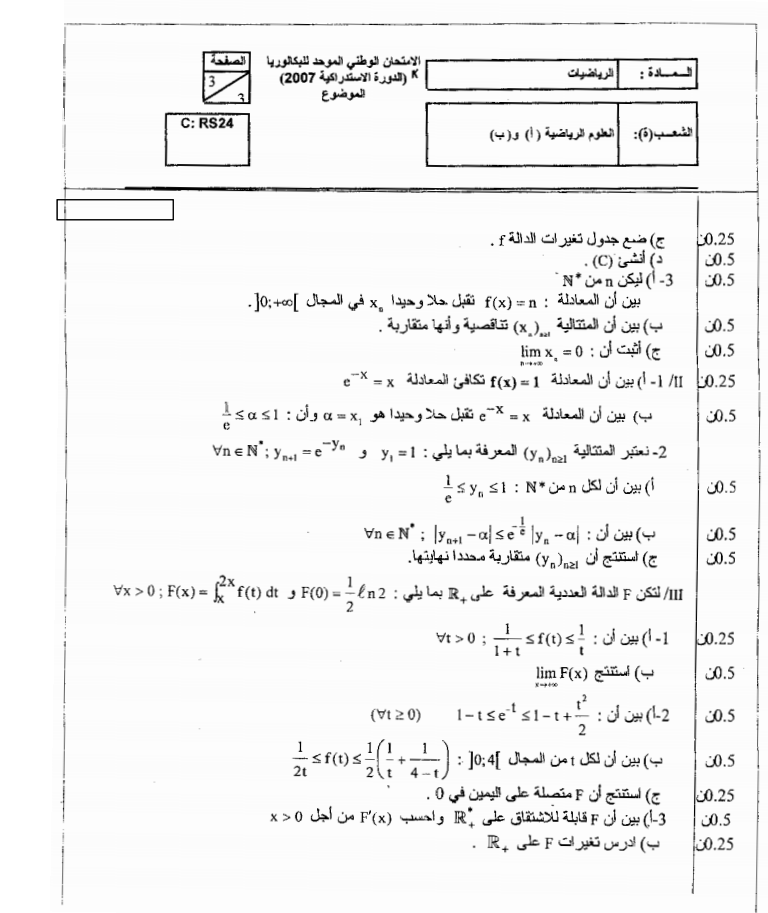
الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 14 - تصحيح موضوع الدورة العادية 18 2007 0 10 10 0 0 1 x x x x e hx e hx h x e f x gt gt gt gt gt gt gt و 0 10 10 0 0 1 x x x x e hx e hx h x e f x lt lt lt lt lt gt gt x fx gt 0 في آلتا الحالتين لدينا Oi j المنسوب إلى معلم متعامد Cf في المستوى P ممنظم د- إنشاء المنحنى JJG JJG lim 0 لدينا x f x إذن Cf y 0 معادلته بجوار أفقيا مقاربا يقبل lim 0 ولدينا x f x x إذن Cf y x معادلته بجوار مائلا مقاربا يقبل

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 15 - تصحيح موضوع الدورة العادية 18 2007 المتتالية العددية المعرفة بما يلي III n n u لتكن 1 1 n n u u fu n x لدينا 1 ليكن 1 0 1 1 1 0 1 1 0 1 1 1 1 x x x x x x f xx x e x x e x e x e e 2 ln 2 x e f xx x في f x x للمعادلة الوحيد الحل هو x ln 2 إذن f 0 10 ولدينا لدينا 2 أ- ليكن x 2 2 1 1 1 1 x x x x g x f x e e e x fx gt 0 إذن f تزايدية على ولدينا إذن 1 0 0 2 x fx f fx 1 ومنه فإن 0 2 x fx إذن 1 2 1 2 x f x فإن وبالتالي 1 2 x f x حسب مبرهنة التزايدات و f متصلة على المجال 0 ب- لدينا f قابلة للاشتقاق على x c fx f f cx ln 2 ln 2 لدينا المنتهية حيث c محصور بين أن وبما fx f x ln 2 ln 2 f c إذن x و ln 2 1 2 f ln 2 ln 2 و f c ln2 ln 2 فإن 1 2 x fx x لدينا n ليكن un f 01 لأن ln2 ln2 إذن 1 2 n n fu u فإن وبالتالي 1 ln2 ln2 1 2 n u u n n 0 ب- نبين بالترجع أن 1 ln 2 ln 2 2 n nu u n

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 16 - تصحيح موضوع الدورة العادية 18 2007 العلاقة صحيحة من أجل n 0 ليكن n نفترض أن العلاقة صحيحة من أجل n ونبين أنها صحيحة من أجل n 1 لدينا 2 1 1 ln 2 ln 2 2 n n u u و 0 1 ln 2 ln 2 2 n u u n إذن 1 0 1 2 1 ln 2 ln 2 2 n n u u أي 1 1 0 1 ln 2 ln 2 2 n n u u 0 وبالتالي فإن 1 ln2 ln2 2 n nu u n ج- لدينا 1 ln2 1 ln2 2 n n un و 1 1 1 1 lim 0 2 2 n n lt lt لدينا التقارب مصاديق حسب n n u lim ln 2 نهايتها متقاربة متتالية n n u IV نعتبر F الدالة العددية المعرفة على بما يلي 2 0 1 0 0 x t x t F x dt x e F x نعلم أن f تناقصية قطعا على إذن 1 أ- ليكن إذا آان x gt 0 فإن 2 2 2 2 22 2 1 1 2 2 2 2 x x x xx x xx x x e e F x xt x f x dt f t dt f x dt x F x x fx f f x ft fx x إذا آان x lt 0 فإن 2 2 2 2 2 2 2 2 2 1 1 2 2 x xx x xx x x x t x fx ft f x f x dt f t dt f x dt xf x x F x xf x F x e e x وبالتالي فإن 2 2 2 2 1 1 x x x x e e x F x

الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 17 - تصحيح موضوع الدورة العادية 18 2007 2 2 ب- لدينا 2 2 1 1 x x x x e e x Fx وبما أن 2 0 0 2 2 1 1 0 0 1 2 2 lim lim 1 x x x x x x e e x x e و 2 0 0 1 0 0 1 lim lim 1 x x x x x e x x e 0 فإن lim 0 0 x Fx F وبالتالي فإن F متصلة في 0 2 2 ج- لدينا 2 2 1 1 x x x x e e x Fx إذن 2 0 1 2 1 x x x F x F x x e x e وبما أن 0 0 2 2 1 1 2 1 1 2 2 lim lim 1 x x x x x e e x x e و 0 0 1 1 1 1 1 lim lim 1 x x x x e x x e فإن 0 lim 1 x F x F x ومنه فإن F قابلة للاشتقاق في0 و F0 1 ليكن -أ 2 لدينا x 1 t t t e f حسب 2 x x أو x 2x المجال على متصلة دالة 6 x 2x المجال على أصلية دالة تقبل فهي x إشارة 2 x x أو و x x fx إذن 2 2 2 1 x x t x x t F x dt t x x e على للاشتقاق قابلتين x 6 2x و لدينا و x x 2 x لدينا و لكل إذن F قابلة للاشتقاق على 2 2 4 2 2 1 1 1 2 2 x x x x x e x e e e F x x x x x fx fx 4 1 3 1 1 x x x e e F x fx fx e وبالتالي فإن 3 1 x x e x Fx fx e ب- نعلم أن f متصلة وتناقصية قطعا على المجال lim lim 0 إذن x x f fx fx gt x fx 0 فإن ومنه 3 وبما أن 1 x x e x Fx fx e x e هي إشارة 3 فإن إشارة Fx على 30 3 ln 3 x x e e x وتزايدية قطعا على آل من المجالين 0ln3 و إذن F تناقصية قطعا على المجال ln3 النهاية
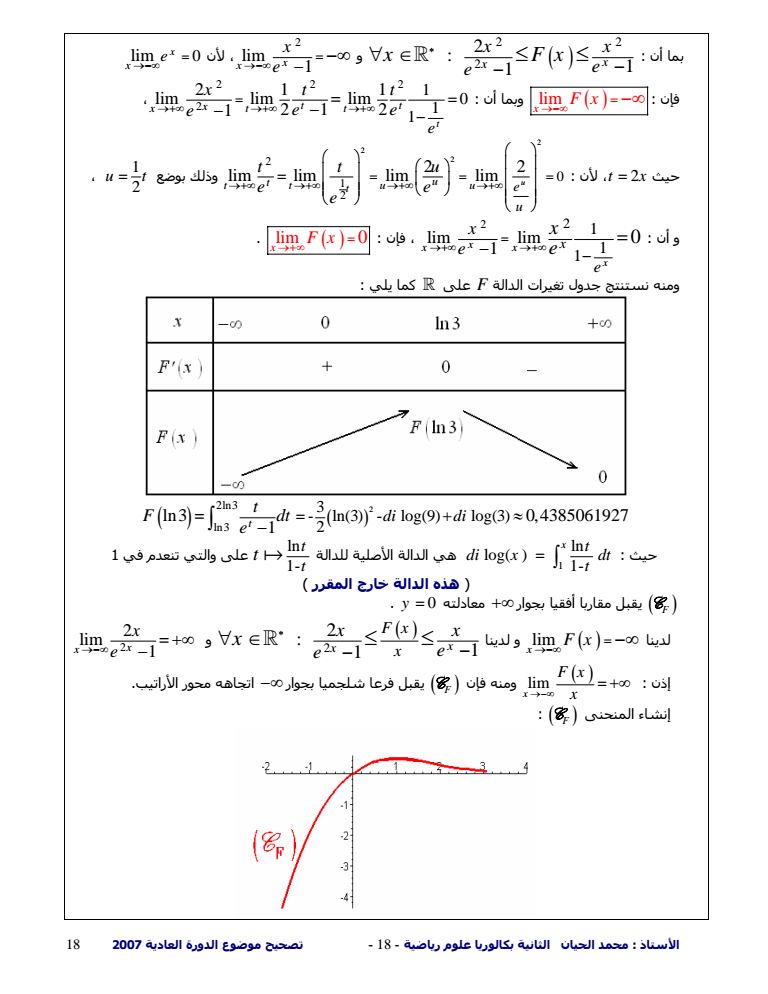
الأستاذ محمد الحيان الثانية بكالوريا علوم رياضية - 18 - تصحيح موضوع الدورة العادية 18 2007 2 2 بما أن 2 2 1 1 x x x x e e x Fx و 2 lim 1 x x x e lim x 0 لأن x e lim فإن x F x وبما أن 2 22 2 1 0 1 1 21 1 lim lim lim 1 2 2 1 t x t t xt t e x tt e e e لأن t x 2 حيث 2 2 2 2 1 2 0 2 2 lim lim lim lim t u u tt u u t e u tt u e e e 1 وذلك بوضع 2 u t و أن 2 2 1 1 1 lim lim 1 0 x x x x x e x e x e lim 0 فإن x F x ومنه نستنتج جدول تغيرات الدالة F على آما يلي 2 2ln3 ln3 3 - ln3 - log9 log3 2 ln3 04385061927 1 t di di t F dt e 1 حيث ln log 1- x t di x dt ln هي الدالة الأصلية للدالة t 1- t t t 6 على والتي تنعدم في 1 هذه الدالة خارج المقرر يقبل مقاربا أفقيا بجوار معادلته CF y 0 lim لدينا x F x و لدينا 2 2 1 1 x x F x x x x e e x 2 و 2 lim 1 x x x e limx إذن F x ومنه فإن CF يقبل فرعا شلجميا بجوار اتجاهه محور الأراتيب x CF إنشاء المنحنى



- 1 - ثانوية محمد الخامس - القنيطرة - تصحيح الامتحان الوطني الموحد الثانية علوم رياضية الأستاذ محمد غريز لدورة يوليوز 2007 أ و ب الاستدراآية التمرين الاول 1 - أ - x ap x bq S 2 لدينا pq1 إذن حسب Bezout 00 0 0 u v pu qv 1 ليكن - ب 0 0 0 x bpu aqv qv 1 p 0 فان pu qv 1 0 0 أن بما و x aqv p 0 0 لدينا 1 x ap 0 ومنه aqv a p 0 اذن لدينا 0 0 0 x bp q 0 اذن x bpu aqv فان pu qv 1 0 0 أن بما و 0 bpu b q 0 اذن pu 1 q 2 x bq 0 منه و من 1 و 2 نستنتج أن x0 حل للنظمة S 2 - ليكن x حلا للنظمة S لدينا x ap x bq و x ap x bq اذن 0 أي x x 0p 0 و x x 0q 2 0 x x mp mn x x nq q m Gauss مبرهنة حسب فانه p q 1 أن بما و q x x q mp 0 m kq 1 اذن 1 k أن وبما 0 x x 0 العدد يقسم pq العدد اذن x x k pq 0 1 فان x x mp 3 0 x x - ليكن x عددا صحيحا نسبيا بحيث pq يقسم العدد k x x kpq 0 اذن x x 0 pq 0 لدينا اذن x x kpq kqp 0 اذن 0 أي qx x 0 و p x x x xp x xq وبما أن x 0 حل للنظمة S فان x ap x bq اذن x ap x bq اذن x حل للنظمة S لدينا - 4 0 0 0 S للنظمة حل x bpu aqv 0 x x pq اذن حلول النظمة S هي الأعداد النسبية x بحيث 5 - لدينا x 18 x 3 13 8513-31 بحيث u v 5 3 0 0 اذن بينهما فيما أوليان 13 و 8 العددين أي x bpu aqv 0 00 لدينا 0 x 3 8 5 1 13 3 120 39 اذن 0 S للنظمة حل x 81 و بالتالي مجموعة حلول النظمة S هي الاعداد النسبية x بحيث x 81 104

- 2 - التمرين الثاني ليكن n عددا صحيحا طبيعيا فرديا أآبر من أو يساوي 3 لدينا n صندوقا مرقما من 1 إلى n الصندوق رقم 1 k n k يحتوي على آرة k بيضاء و n-k آرة سوداء 1 - ليكن B الحدث الكرة المسحوبة بيضاء لكل k من 12n نضع Ek الحدث اختيار الصندوق رقم k k p و E E E 12 n لدينا E E k p 12 n pB pB pB E E E 12 n pB pB E B E B E 12 n pB pB E B E B E k لدينا k E k pB E p B pE اذن k k kE pB E pE p B اذن 12 n 1E 2E n E pB pE p B pE p B pE p B لدينا 12 n 1 pE pE pE n و E k k p B لان الصندوق رقم k يحتوي على k آرة بيضاء n اذن 1 1 2 n 1 nn 1 pB n n n n n 2n بالتالي و n 1 pB 2n 2 - ليكن I الحدث الصندوق يحمل رقما فرديا 2k 1 1 k 1 لدينا n فردي n2k1 عدد الصناديق التي تحمل رقما فرديا هو 2 1 اذن k 1 1 n C k 1 pI C n فإن n 2k 1 أن وبما n 1 k 2 اذن n 1 1 2 pI n بالتالي و n 1 pI 2n 3 I - احتمال الحصول على آرة بيضاء علما أن السحب تم من صندوق رقمه فردي هو pB I p B pI I E E E E 135 n لدينا اذن 135 n pB I pB E E E E 13 n pB E B E B E 13 n pB E B E B E اذن 13 n 1E 3E n E pB I pE p B pE p B pE p B 11 13 1n pB I nn nn nn 2 1 pB I 1 3 5 n n 1 3 5 n 1 3 5 2k 1 أن بالترجع نبين أن يمكن n 2k 1 لان 2 2 n 1 k 1 2 2 اذن 2 1 n1 pB I n 2 اذن 2 I 2 n 1 2n p B 4n n 1 I بالتالي و n 1 p B 2n

- 3 - التمرين الثالث المجموعة نعتبر 2 2 2 H Mz P z z z 1 z x iy ليكن - أ - 1 2 2 2 M H z z z 1 22 22 22 x y 2ixy x y 2ixy x y 1 1 2 2 x 3y 1 1 هي معادلة ديكارتية للمجموعة H 2 2 ب - بما أن معادلة المجموعة H هي 2 2 x y 1 1 1 3 O00 مرآزه هذلول H فان ومقاربيه A 10 و A10رأسيه و 3 y x 3 و 3 y x 3 z x iy و z x iy بحيث H من نقطتان M z و M z لتكن - 2 zz zz zz zz نضع zz xx yy ixy xy و zz xx yy ix y xy لدينا z z xx 3yy ixy x y اذن zz xx yy ixy xy و لدينا 2 2 2 2 22 22 22 xx 3yy 3xy x y x x 9y y 3x y 3x y فان Hمن نقطتان M z و Mz أن بما 2 2 و x 3y 1 2 2 x 3y 1 اذن 2 22 2 أي x 3y x 3y 1 2 2 22 22 22 x x 9y y 3x y 3x y 1 M z z H بالتالي و لدينا و z1 z 1 z 1 z 1 z لدينا - ب 2 2 2 zz z z z z z z zz z فان Mz H أن وبما 2 2 2 zz 1 منه و zz z 1 MzMz M z z H من Mz و Mz لكل حيث الداخلي الترآيب بقانون H نزود - 3 Mzquot و Mz و Mz لكل MzMz Mzquot MzM z z لدينا MzMzz zzquot zzquot M zzzquot zzquot zzquot Mzzzquot zzquot zzquot zzzquot zzquot zzquot zzzquot zzzquot zzzquot Mzz zquot zz zquot zz zquot zz z zz zquot 1

- 4 - MzMz Mzquot Mzz zz zz Mzquot M zz zz zz zquot Mzz zquot zzquotzquot zz z zz zquot zz zquot zz zquot zz zquot zz z zz zquot Mzzzquot zzzquot zzzquot zzzquot zzz 2 MzMzMz MzMzMz أن نستنتج 2 و 1 من اذن القانون تجميعي MzMz M zz Mzz zz zz لدينا Mz Mz M z z Mz z z z zz و Hمن Mz و Mz لكل MzMz Mz Mz اذن اذن القانون تبادلي Hمن Mz لكل MzM1 Mz أي M z1 Mz لدينا اذن M1 هو العنصر المحايد للقانون MzMz M1 اذن M zz M1 لدينا اذن آل عنصر Mz من H يقبل مماثلا في H هو Mz و بالتالي H زمرة تبادلية التمرين الرابع 2 ab b F Mab ab 5b a 3b O M00 و J M01 و I M10 نضع O F لان F و F M 2 - أ - 1 Ma b Mcd Ma c b d F F من Mcd و Mab لكل اذن F زمرة جزئية من الزمرة التبادلية M R 2 اذن F زمرة تبادلية Mab F R M aI bJ aI bJ اذن M F اذن F جزء مستقر بالنسبة للقانون الخارجي F M 2 و M 2 R فضاء متجهي حقيقي فان الخاصيات الأربع تبقى متحققة بما أن R M M M M 2 MM F M M M 2 M F R M M M F 1M M اذن F فضاء متجهي حقيقي F الحقيقي المتجهي للفضاء مولدة IJ الأسرة اذن M F Mab aI bJ لدينا - ب 0 0 5 3 00 0 0 I J 0 0 2 اذن الأسرة IJ حرة ومنه الأسرة IJ أساس للفضاء المتجهي F dim F 2 اذن 2 هو IJ الأساس عناصر عدد 2 - ليكن عددا عقديا لا ينتمي إلى حيث x iy 1 1 نضع 1 1 x y

- 5 - بحيث 2 z x iy لكل z من يوجد زوج وحيد x y من بحيث z 2 هل يوجد زوج وحيد من 1 1 x iy x i y 1 1 x iy x iy 1 1 1 y y x y x y 1 1 x x y y 1 1 1 x x y y y y من وحيد زوج يوجد من z لكل 2 z 1 بحيث و بالتالي 1 أساس للفضاء المتجهي F - 3 za b حيث من z عنصر لكل z z Mab 2 ab 1 1 أ - لدينا J 5 3 اذن 2 4 2 J 10 4 2 1 و لدينا I J 5 2 اذن 2 J 2I J M01 J اذن 0 1 لدينا من عنصران z a b و za b ليكن - ب zz a ba b لدينا 2 aa ab a b bb z z Ma b Ma b ولدينا aI bJ a I b J 2 aa I ab a bJ bbJ aa I ab a bJ bb 2I 2J aa 2bbI ab a b 2bbJ Maa 2bb ab a b 2bb aa 2bb ab a b 2bb يكون أن يجب تقابليا تشاآلا يكون لكي 2 aa ab a b bb aa 2bb ab a b 2bb اذن 2 أي bb 2bb 2 bb 2 2 20 1 i أو 1 i اذن 12 1 لدينا 1 i نأخذ - 4 و J لدينا 2007 مرة2007 F نحو من تشاآل لان اذن 2007 اذن 2007 2007 J حسب صيغة Moivre لدينا 2007 2007 2007 2007 33 3 3 1 i 2cos isin 2 cos 2007 isin 2007 44 4 4 اذن 1004 1004 2007 2007 2007 222 2 2 cos isin 2 i i 4 4 22 2 2

- 6 - اذن 2007 1003 1003 1003 1003 1004 1003 2 i2 2 1 i 2 1 i 2 2 2 1 i 2007 1004 1003 2 2 a b Mab أي z Mab أن نعلم 2007 2007 1004 1003 2007 J 2 2 J 1004 1003 2007 M 2 2 J 2007 1004 1003 J 2 I2 J التمرين الخامس - 1 I x gx 1 x e - أ x g x 1 x e 0 على قطعا تزايدية g اذن x x ب - x x lim gx lim 1 x e x x 1 lim 1 x1 xe x x x lim gx lim 1 x e x 0 gx gx x ج - g متصلة و تزايدية قطعا على و lim gx x و lim gx اذن g تقابل من نحو فان g0 0 أن بما و 0 gx 0 للمعادلة الوحيد الحل هو x 0 لدينا - 2 x 1 fx 1xe x أ - 1 lim f x 0 x و 1 lim f x 0 x x x0 x0 x0 x0 x0 x0 x 1 1 lim f x lim lim 1xe e 1 x e و x x0 x0 x0 x0 1 lim f x lim e 1 x x x ب - لدينا x x2 2 1 x e g x f x 1 x e g x f x 0 فان g x 0 أن بما - ج x 0 fx - - fx

- 7 - د - 3 - أ - ليكن n من لدينا hx fx n لتكن x x lim hx lim f x n n و x 0 lim hx n h x f x 0 x على قطعا تناقصية h اذن فان h تقابل من 0 نحو n بما أن متصلة و تناقصية قطعا على n hx 0 اذن يوجد عدد حقيقي وحيد xn من0 بحيث اذن المعادلة fx n تقبل حلا وحيدا xn في المجال0 لدينا - ب n fx fx n1 n اذن fx n 1 n 1 و fx n اذن المتتالية x n تناقصية n1 n x x وبما أن f تناقصية قطعا على 0 فان لدينا n 0 بالعدد مصغورة x n اذن x 0 و بما أن x n تناقصية و مصغورة بالعدد 0 فان x n متقاربة n ج - لتكن n lim x A n n x n 1 fx n n 1x e n x n 1 1x e n 1 e0 A A n x n n n 1 lim 1 x e lim n 1 e A A نفترض أن A 0 e 1 أي A 0 و 1 1 A اذن A e 1 و 1 1 A اذن A ممكن غير n بالتالي و A 0 اذن n lim x 0 - أ - 1 II x 1 fx 1 1 1xe x 1xe 1 x e x ب - حسب س 3 - أ - المعادلة fx 1 تقبل حلا وحيدا x 0 1

- 8 - 1 1 لنبين أن e على متصلة u لدينا ux fx 1 لتكن 1 1 e قطعا تناقصية u اذن u x f x 0 و 1 1 e لدينا 1 u1 u 0 e 1 1 تقبل حلا وحيدا x e x اذن حسب مبرهنة القيم الوسطية المعادلة e لدينا - أ - 2 1 و y 1 n y n 1 y e لدينا n 1 أجل من 1 1 اذن y 1 1 y 1 e n نفترض أن 1 y 1 e و نبين أن n 1 1 y 1 e n لدينا 1 y 1 e n اذن 1 1 y e 1y0 n أي اذن n 1 y ee 1 n 1 أي 1 y 1 e n و بالتالي 1 y 1 e n f متصلة على المجال المغلوق الذي طرفاه و x fx e yn ب - لتكن n y و قابلة للاشتقاق على المجال المفتوح الذي طرفاه و n y اذن حسب مبرهنة التزايدات المنتهية يوجد عدد حقيقي c محصور بين و بحيث n n y f c y n1 n اذن f y f f c y لدينا x f x e اذن c f c e أي c f c e لدينا n اذن c y n y c 1 1 و بما أن e فان 1 1 e 1 اذن c e 0e e e 1 و بالتالي e n1 n y ey n 1 ج - لدينا e 2 1 y ey 1 e 3 2 y ey 1 e n n1 y ey 1 اذن e n 1 n 1 y e y منه و n 1 n 1 1 e 1 y y e بما أن n 1 1 n e 1 lim 0 e و متقاربة y n فان n n lim y بما يلي III لتكن F الدالة المعرفة على 2x x Fx f tdt x 0 1 F0 ln 2 2 أي t 0 اذن t 0 لدينا - أ - 1 t e 1 اذن t te 1t أي t t 1te t اذن 1 1 1te t أي 1 ft t 1

- 9 - لدينا t e 0 اذن t 1te 1t إذن t 1 1 1 t 1te أي 1 ft 1 t 2 أن نستنتج 2 و 1 من 1 1 ft 1t t t 0 لدينا - ب 1 1 ft 1t t اذن 2x 2x x x xx 1 1 dt f tdt dt 1t t x 0 ln1 2x ln1 x Fx ln2x lnx اذن اذن 1 2x 2x ln Fx ln ln2 1x x x و بما أن 1 2x lim ln ln 2 1 x x فان lim Fx ln 2 أن لنبين - أ - 2 2 t t 1t e 1t 2 t 0 و ut 1 t لتكن t vt e v0 1 و u0 1 و 0 على للاشتقاق قابلتان دالتان v و u t vt e t 0 u t 1 و أي t 0 اذن t 0 لدينا t e 1 اي t 1 e u t vt أي 1 t 0 لكل ut vt اذن 2 لتكن t wt 1 t 2 u0 1 و w0 1 لدينا t 0 w t 1 t فان ut vt أن بما t 1t e أي t e 1t vt w t اذن 2 t 0 لكل vt wt منه و ut vt wt أن نستنتج 2 و 1 من بالتالي و 2 t t 1t e 1t 2 t 0 لدينا - ب t 1t e t 0 لكل اذن t 1e t أي t 1 t e 2t اي t 1 1 2t 1te اذن 1 ft 2t 1 t لدينا 11 1 11 1 1 ft 2t 4 t 2t 4 t 1te 2 t t 2 2t t 2e t4 t1 t e أن بما 2 t t e 1t 2 فان 2 t 2 2t t 2e 0 فان t 0 لكل ft 0 أن بما و t 1te 0 0t4 لان t4 t 0 لدينا و اذن 11 1 ft 2t 4 t 2 أن نستنتج 2 و 1 من 1 11 1 ft 2t 2 t 4 t 04 من t لكل

- 10 - لدينا - ج 1 11 1 ft 2t 2 t 4 t اذن 2x 2x 2x xx x 1 11 1 dt f tdt dt 2t 2 t 4 t أي 2x 2x x x 1 1 ln t Fx lnt ln4 t 2 2 أي ln 2 ln 2 1 4 2x Fx ln 2 2 2 4x x 0 و بما أن 4 2x lim ln ln1 0 4 x فان x 0 ln 2 lim Fx F0 2 x 0 0 في متصلة F اذن 3 2x - أ - لدينا x Fx f tdt f متصلة على x2x اذن f تقبل دالة أصلية على x2x بحيث قابلة للاشتقاق على x 0 x2x x f x و 2x لدينا x Fx t 2x x x2x على للاشتقاق قابلة x x الدالة الدالة x 2x قابلة للاشتقاق على x2x لأنها مرآب دالتين قابلتين للاشتقاق اذن F قابلة للاشتقاق على x2x حيث x 0 اذن F قابلة للاشتقاق على Fx 2x2 x 2f 2x f x x 2x x 2 1 Fx 1 2x e 1 x e 2x x x 2x 2x 2 1 1 e e e 2e 1 gxg2x e gxg2x x 2 2x e 1 Fx e gxg2x لدينا - ب x 2 من x لكل g2x 0 و gx 0 و e 1 0 اذن F تزايدية قطعا على

SUJET DE BACCALAURAT MAROC Juin 2006 EPREUVE DE MATHEMATIQUES FILIERE SCIENCES MATH La dure de lpreuve est de 4 heures coefficient 10 et lusage des calculatrices NON programmables est autoris Exercice 1 35 Points On note G lensemble des matrices de M 2 scrivant sous la forme avec 1 0 M a b a b a b On rappelle que est un anneau unitaire 2 M Partie I 1 Montrer que G est une partie stable de M 2 2 Montrer que G est un groupe Ce groupe est-il commutatif 3 Soit H lensemble des matrices de G telles que M a b a b Montrer que H est un sous groupe de G 4 Soit A un lment de G tel que 1 0 1 A a a On pose et 1 A A 2 A A A A n 1 n A A pour tout entier naturel non nul n Donner lexpression de en fonction de et de n A a n Partie II Pour tout a b et x y dans on dfinit la loi de composition interne T par a bT x y a bxby Soit lapplication dfinie de G vers par a b on a M a b a b 1 Montrer que est un morphisme bijectif de G vers T 2 En dduire la structure algbrique de T 1

3 Pour tout rel et pour tout entier naturel dterminer le symtrique de dans a n 2 n fois a T 1 a T 1 a1T T EXERCICE 2 25 Points On considre dans lquation 2 2 2 x x y y x y on note E cette quation 1 Soit le couple x y une solution de E On pose d P GCD x y x a d et y bd a Vrifier que 2 2 d b a b a ba 2 b En dduire que b 1 c Montrer que a 1 et que a 1 divise 1 a d En dduire que a 2 ou a 3 2 Rsoudre dans lquation E EXERCICE 3 5 Points Pour tout nombre complexe z on pose 2 P z z 2 6iz Partie I Dans le plan complexe est rapport un repre orthonorm O e 1 e 2 JJG JJG on considre lensemble des points M daffixe z tels que P z est imaginaire pur On note H cet ensemble 1 Montrer que 0 est une quation cartsienne de 2 2 x y 2 6 x y H 2 Montrer que est une hyperbole puis dterminer son centre ses sommets ainsi que deux quations de ses asymptotes dans le repre H O e 1 e 2 JJG JJG 3 Vrifier que le point Origine du repre est un point de puis donner une quation cartsienne de la tangente au point dans le repre O H H O O e 1 e 2 JJG JJG 4 Tracer H dans le repre 1 2 O e e JJG JJG Partie II 1 Rsoudre dans lquation P z 4 6i 2 On pose u i 1 5 v i 1 w i 239 1 arctan 5 et 1 arctan 239 2

a Vrifier que 4 u v 4w b Exprimer un argument de u en fonction de et un argument de w en fonction de c En dduire que 1 1 4arctan arctan 5 239 4 EXERCICE 4 9 Points Partie I Dans cette partie n est un entier naturel suprieur ou gal 3 On considre la fonction dfinie sur n g par 2 ln n g x n x x 1 Dresser le tableau de variations de n g 2 Montrer que pour tout on a x x gt lnx 3 a Montrer que lquation 0 n g x admet dans une unique solution note n puis montrer que 1 1 n n n lt lt b En dduire que lim 0 n n Partie II I Soit f la fonction dfinie sur 0 par 3 x f x x e On note sa reprsentation graphique dans un repre orthonorm Cf O i j G G On prend i j 3 G G cm 1 Etudier la drivabilit de f droite de zro puis donner une interprtation gomtrique de ce rsultat 2 Calculer lim x f x puis donner une interprtation gomtrique de ce rsultat 3 a Montrer que pour tout rel x appartenant 0 1 3 3 x f x f x x b Dresser le tableau de variations de f 4 Tracer On prendra Cf 1 05 3 f II On pose 1 1 3 I 3

1 a Montrer que f I I b A laide de la question 3a de la Partie II montrer que 2 3 x I f x c Montrer que 3 x 0 x f gt et x x o 3 est la solution de lquation Cf Partie I 3 g x 0 2 Soit la suite dfinie par 0 n n u 1 3 u et pour entier naturel n 1 n n u f u a Montrer que pour entier naturel n n u I b Montrer que pour entier naturel n 1 3 3 2 3 n n u u c En dduire que pour entier naturel n 1 3 2 3 n n u d Montrer que la suite est convergente et donner sa limite 0 n n u Partie III Soit F la fonction dfinie sur 0 par 8 x x F x f t dt 1 a Montrer que F est drivable sur 0 b Donner lexpression de pour tout F x x appartenant 0 et en dduire le sens de variations de F 2 a Montrer que pour tout x appartenant 0 on a 7 0 2 1 x F x f x e b En dduire la valeur de lim x F x c Dresser le tableau de variations de F FIN DU SUJET 4

1 hf1n ahf h 2006fhf إنجاز محمد أيت الحسين أستاذ بثانوية مولاي رشيد فاس ana Xiy لكل لدينا 1 4 b 0 و b 0 بحيث aa bb ab a b 10 1 0 M M a b a b a ba bb 1 0 M a ba bb فإن bb 0 أن بما قي مستقرة G ومنه M G a ba bb 2 M 2 المصفوفة 1 0 I 0 1 تحقق 01 العنصر هو I إذن I M المحايد ل G ليكن 2 det M b 0 ab لدينا b 0 بحيث ab M وهو 2 تقبل مقلوبا Mab في إذن 1 ab 1 b 0 M b a 1 أن نلاحظ 1 ab a 1 b b M MG تجميعي في M2 إذن فيG بالأحرى من كل ما سبق نستنتج أن G زمرة aa b بحيث 3 b 0 حسب ما سبق أعلاه لدينا لكل إذا وفقط إذا MM M M ab a b a b ab إذا وفقط إذا a ba a ba a a أو b 1 أي a a 1 b 0 aa b بحيث 3 يكفي إذن أن نختار تكون لكي a a و b 1 MM M M ab a b a b ab نجد aa b 01 1 مثلا MM M 0 1 1 1 1 1

2 و MM M 1 1 0 1 1 1 إذن الزمرة G ليست تبادلية لأن H و H G 3 M H 01 لكل 2 لدينا bb b 0 gt و b 0 bb 0 gt gt إذن H مستقرة قي G lt lt 1 b0 0 b و لدينا لكل عدد حقيقي b إذن 1 ab ab a 1 b b M H M M H إذن H مستقرة بالمقلوب ومنه H زمرة جزئية للزمرة G لدينا 4 2 10 10 1 0 A a 1 a 1 2a 1 أن بالترجع لنبين n 1 0 Pn A na 1 لدينا P1 صحيحة نفترض أن Pn إذن 1 0 n 1a 1 n1 n 1 0 10 A AA na 1 a 1 ومنه n 1 0 n A na 1 Xi1 1 معرف لأن 2 2 ab a b aa bb M M ab a b له سابقا Mab يقبل ab لأن شمولي تبايني لأن ab a b ab a b M M ab a b M M إذن تقابل لكل لأن تشاكل 2 2 aa bb ab a b a ba bb ab a b MM M a ba bb abTa b M TM
3 T زمرة غير تبادلية لأنها صورة زمرة غير تبادلية 2 بتشاكل تقابلي M 01 01 ملاحظة العنصر المحايد لهذه الزمرة هو ومماثلab هو 1 ab a 1 b b a 1 ab M M b b 3 a1 a1 a1TTa1 M TT M n M M M a1 a1 a1 1 M M na1 na1 M na1 na1 ملخص a1TTa1 na1 Zbrana 1 أ بالتعويض المباشر نجد 22 22 2 a d ad bd b d ad bd وبما أن d 0 فإن 2 22 a a b b da b 3 d اختزلنا ب ba ba و بما أن d xy فإن 2 ب لدينا حسب أ a b1 ومنه حسب مبرهنة كوص ab1 2 ومنه أيضا ba b b a إذن ba b ومنه ab b أي b 1 ج تصبح المتساوية أعلاه في أ 2 2 da 1 a 1a a 1 a 1 أو a 0 ومنه هذا يعني بالخصوص أن العبارة a 1 خاطئة إذن a 1 إذن لدينا 2 a 1a 1a

4 ونعلم أن a 1 a 1 حسب متطابقة بوزو والعلاقة سبق كما إذن a a 1 1 2 حسب ومنه a 1 a 1 مبرهنة كوص a 1a 1 د لدينا a 1a 1 a 1a 1 a 1 a 1a 1 a 12 ومنه a 1 12 فإن a10 gt أن وبما a 3 أو a 2 أي 2 لدينا حسب ما سبق إذا كان xy حلا للمعادلة E فإنه يوجد d بحيث 2 2 x da y d a 23 da 1 a 1a d 12 فإن a 2 كان إذا d 9 فإن a 3 كان إذا xy 242279 ومنه بإنجاز الحساب تحققنا من كون الزوجين أعلاه حلين للمعادلة ومنه مجموعة الحلول S 242279 Zsbrana Xiy بحيث z x yi نضع 1 2 لديناxy Mz H RePz 0 2 2 Rex y 2ixy 2 6ix yi 0 2 2 2 2 Rex y 2x 6y i2xy 6x 2y 0 x y 2x 6y 0 ومنه 2 2 x y 2x 6y 0 معادلة ديكارتية ل H

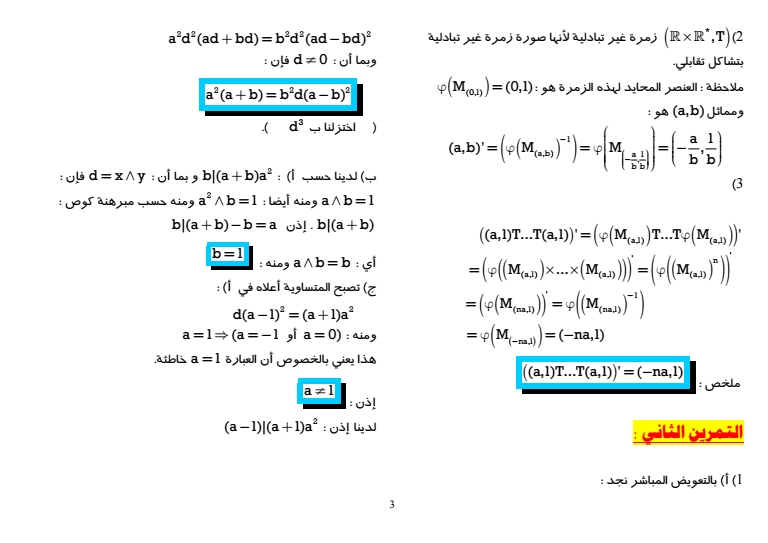
5 2 لدينا 22 2 2 2 2 2 2 x y 2x 6y 0 x 1 y 3 8 X Y 1 8 8 بحيث X x1 Y y3 ومنه H هذلول مركزه هو 13 و 2 2 2 2 X Y 1 8 8 المعلم في له معادلة 1 2 e e JJG JJG الرأسان لدينا ab 8 ومنه الرأسان A 0 8 و e e1 2 المعلم في A 0 8 JJG JJG و A 13 8 أي e e1 2 المعلم في A 33 8 JJG JJG المعلم في المقاربين معادلتا المقاربان 1 2 e e JJG JJG D Y X و D Y X المعلم في معادلتيهما ومنه Oe e1 2 JJG JJG D y 3 1 x و D y 3 x 1 D y 3 x 4 و Dy x 2 أي ملحوظة لم تطلب العناصر المميزة لكن نعطيها إتماما للفائدة ومنه ab 8 لدينا 2 2 c ab 4 ومنه التباعد المركزي c 4 e 2 a 8 البؤرة F04 الدليل المرتبط بها 2 a Y 2 c البؤرة F0 4 الدليل المرتبط بها 2 a Y 2 c المعلم في 1 2 e e JJG JJG 4 الإنشاء انظر الشكل أسفله Xi1 تكافئ Pz 4 6i المعادلة 1 2 z 2 6iz 4 6i 0 هو المختصر مميزها 2 2 1 3i 4 6i 4 2i جذراها ومنه 1 و z 1 3i 2i 1 i 2 z 1 3i 2i 1 5i
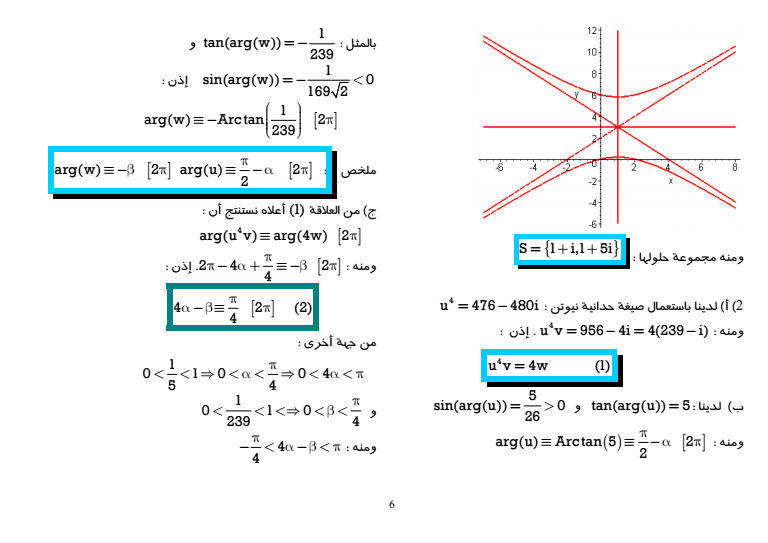
6 حلولها مجموعة ومنه S 1 i1 5i 2 4 u 476 480i أ لدينا باستعمال صيغة حدانية نيوتن ومنه 4 إذن u v 956 4i 4239 i 4 u v 4w 1 و tanargu 5 لدينا ب 5 sinargu 0 26 gt argu Arc tan 5 2 ومنه 2 بالمثل 1 tanargw 239 و 1 sinargw 0 169 2 إذن lt 1 argw Arc tan 2 239 argu 2 ملخص 2 argw 2 ج من العلاقة 1 أعلاه نستنتج أن 4 argu v arg4w 2 24 2 ومنه 4 إذن 4 2 2 4 من جهة أخرى 1 0 1 0 04 5 4 lt lt lt lt lt lt و 1 0 10 239 4 lt ltlt lt lt 4 ومنه 4 lt lt

7 k 4 k2 أن نستنتج أعلاه 2 ومن 4 ومن المتفاوتة المزدوجة أعلاه نحصل على k2 4 4 أي lt lt 1 3 k 2 4 k 0 ومنه lt lt 4 إذن 4 ومنه 1 1 4Arc tan Arc tan 5 239 4 iaana Xiy لدينا 1 n 2 x 0 g x n 0 x gn الدالة ومنه gt gt تزايدية قطعا على 0 ومنه جدول تغيراتها لدينا x ux x ln x 6 الدالة تغيرات لندرس 2 11 x x 0 u x x 2 2 x 2x x x gt u x 0 x 4 و u x 0 x 4 gt gt منه و وهذا يعني بالخصوص أن u4 قيمة دنيا مطلقة للدالة u x 0 ux u4 2 ln4 21 ln2 0 gt gt إذن قطعا تزايدية ln و e 2 gt و 1 ln2 lne ln2 لأن إذن x x ln x 0 gt لة وتزايدية قطعا المجال gn I 0 متص على 3 أ الدالة لدينا حسب السؤال I g I n 1 نحو gn تقابل من إذن g I n n I ب gn في بالخصوص 0 يقبل سابقا وحيدا n لدينا 1 g n lnn 0 n gt 2 السؤال حسب n و 1 g 1 2lnn 0 n lt أن يعني هذا n 3 لأن lt lt n nn n 1 1 gg g n n
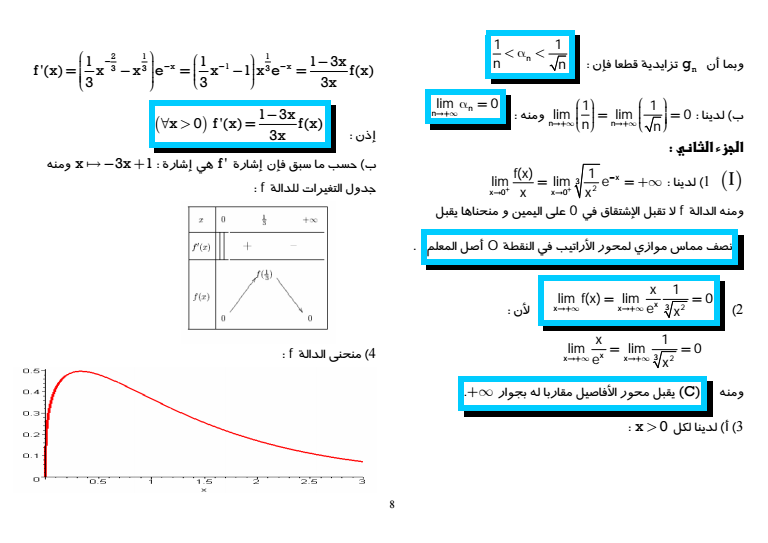
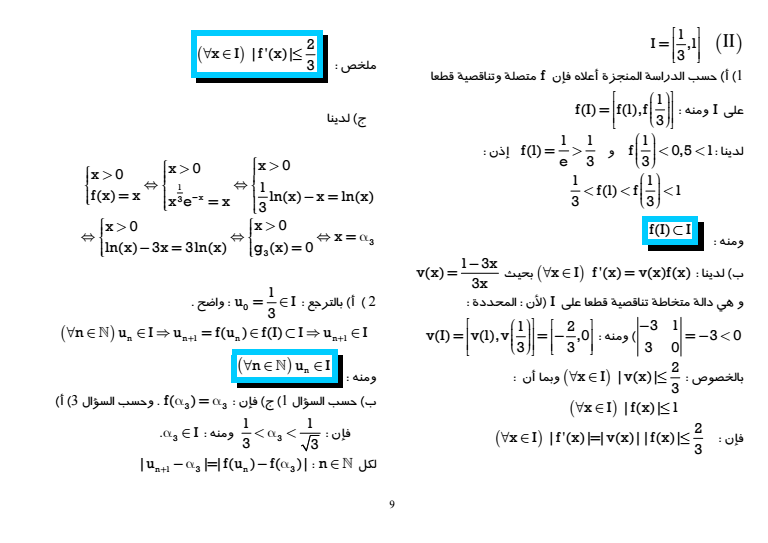
8 gt n gt تزايدية قطعا gn فإن وبما أن 1 1 n n ب لدينا n n 1 1 lim lim 0 n n ومنه n nlim 0 Xi1 لدينا 1 I 3 2 x x0 x0 fx 1 lim lim e x x ومنه الدالة f لا تقبل الإشتقاق في 0 على اليمين و منحناها يقبل نصف مماس موازي لمحور الأراتيب في النقطة O أصل المعلم 2 x x x 3 2 x 1 lim fx lim 0 لأن e x x x x 3 2 x 1 lim lim 0 e x ومنه C يقبل محور الأفاصيل مقاربا له بجوار 3 أ لدينا لكل lt x 0 21 1 1 1 1 3x 33 3 x1 x f x x x e x 1 x e fx 3 3 3x إذن 1 3x x 0 f x fx 3x gt ب حسب ما سبق فإن إشارة f هي إشارة x 3x 1 6 ومنه جدول التغيرات للدالة f 4 منحنى الدالة f
9 II 1 I 1 3 1 أ حسب الدراسة المنجزة أعلاه فإن f متصلة وتناقصية قطعا ومنه I على 1 fI f1f 3 لدينا 1 f 05 1 3 lt lt و 1 1 f1 e 3 إذن gt 1 1 f1 f 1 3 3 ltlt lt ومنه fI I بحيث x I f x vxfx لدينا ب 1 3x vx 3x و هي دالة متخاطة تناقصية قطعا على I لأن المحددة 3 1 3 0 3 0 gt ومنه 1 2 vI v1 v 0 3 3 بالخصوص 2 x I vx 3 أن وبما x I fx 1 فإن 2 x I f x vxfx 3 ملخص 2 x I f x 3 ج لدينا 1 3 x x 0 x 0 x 0 1 fx x lnx x lnx xe x 3 gt gt gt 3 3 x 0 x 0 x lnx 3x 3lnx g x 0 gt gt بالترجع أ 2 0 1 u I 3 واضح n u I u fu fI I u I n n1 n n1 ومنه n uI n ب حسب السؤال 1 ج فإن f 3 3 وحسب السؤال 3 أ 3 فإن 1 1 3 3 3 I ومنه lt lt n لكل u fu f n1 3 n 3
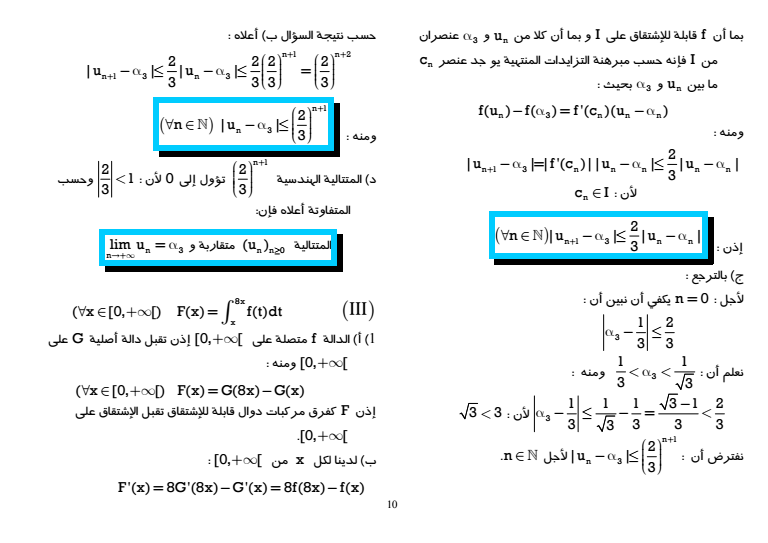
10 3 عنصران و un بما أن f قابلة للإشتقاق على I و بما أن كلا من cn من I فإنه حسب مبرهنة التزايدات المنتهية يو جد عنصر 3 بحيث و un ما بين n 3 nn n fu f f c u ومنه n1 3 n n n n n 2 u f c u u 3 لأن c I n إذن n1 3 n n 2 n u u 3 ج بالترجع لأجل n 0 يكفي أن نبين أن 3 1 2 3 3 أن نعلم 3 1 1 3 3 ومنه lt lt 3 1 1 1 31 2 3 333 3 3 3 lt لأن lt نفترض أن n 1 n 3 2 u 3 n لأجل حسب نتيجة السؤال ب أعلاه n1 n 2 n1 3 n 3 2 22 2 u u 3 33 3 ومنه n 1 n 3 2 n u 3 د المتتالية الهندسية n 1 2 3 لأن 0 إلى تؤول 2 1 3 وحسب lt المتفاوتة أعلاه فإن المتتالية n n0 u متقاربة و n 3 nlim u III 8x x Fx ftdt x 0 1 أ الدالة f متصلة على 0 إذن تقبل دالة أصلية G على 0 ومنه x 0 Fx G8x Gx إذن F كفرق مركبات دوال قابلة للإشتقاق تقبل الإشتقاق على ب لدينا لكل x من 0 F x 8G8x Gx 8f8x fx

11 أي 3 33 8x x x 7x F x 16 x e xe xe 16e 1 3 x 7x x 0 F x x e 16e 1 ومنه 4ln2 x 7 x 0 F x 0 x 0 أو 7x 4ln2 x 0 F x 0 16e 1 x 7 gt gt lt ومنه تغيرات F على قطعا تزايدية F 4ln 2 0 7 على قطعا تناقصية F 4ln 2 7 4ln 2 F 7 F للدالة مطلقة قصوى قيمة لدينا x 8x ومنه 2 أ ليكن x 3 3 3 t x8x t 8x 2 x إذن 8x 8x 3 t t 3 x x Fx t e dt 2 x e dt 8x 3 3 t x 8x x 2 x e 2 xe e 3 x 7x 7x 2 x e 1 e 2fx1 e ومنه Fx 0 فإن x8x على f 0 أن وبما 7x x 0 Fx 2fx1 e أن نعلم ب xlim fx 0 لدينا و 7x xlim 1 e 1 إذن 7x xlim 2fx1 e 0 المزدوجة المتفاوتة وحسب فإن أعلاه xlim Fx 0 ج جدول التغيرات للدالة F




1 المملكة المغربية وزارة التربية الوطنية والتعليم العالي و تكوين الأطر و البحث العلمي قطاع التربية الوطنية الامتحان الوطني الموحد للبكالوريا الدورة العادية 2005 الشعبة العلوم المادةالرياضيات المدة4ساعات المعامل 10 الرياضيةأ و ب التمرين الأول 2 نعتبر في قانون الترآيب الداخلي المعرف بما يلي من x y و a b لكل 2 2 2 ax by ay bx a b x y لتكن اجملموعة 1 1 2 E m m m m m 1 بين أن قانون داخلي في اجملموعة E 1 1 من نحو E بما يلي 2 ليكن التطبيق المعرف m m m m m m نحو E أ بين أن تشاآل تقابلي من ب استنتج أن E زمرة تبادلية محددا عنصرها المحايدومماثل آل عنصر 1 1 m m m m حيث عدد m حقيقي غير منعدم اجملموعة نعتبر 3 2 2 و y x 4 2 F x y x 2 أن بين أ 1 1 2 F m m m 0 m m gt ب بين أن F زمرة جزئية من E التمرين الثاني الجزء الأول p عدد صحيح طبيعي أولي أآبر أو يساوي من 5 1 2 بين ان p 13 2 أ باستعمال زوجية العدد p بين أنه يوجد عدد صحيح طبيعي q بحيث httpmathkasicima

2 2 p q 1 4 q 1 ب استنتج أن 2 p 1 8 3 2 بين أن p 1 24 الجزء الثاني ليكن a عددا صحيحا طبيعيا أوليا مع العدد24 1 2 بين أن a 1 24 طبيعية صحيحة أعداد توجد هل 2 1 a 23 24 1 حيث a k و 123من k لكل a 2 2 1 23 24 و ak للعددين الأآبر المشترك القاسم هو ak 24 a a 23997 التمرين الثالث الجزء الأول نعتبر الدالة العددية f المعرفة على اجملال 0 بما يلي 2 2 0 0 0 x f x x e x f gt O i j ممنظم متعامد معلم في منحناها C f ليكن G G 2cm الوحدة 1 أ بين أن f متصلة على اليمين في 0 ب بين أن f قابلة للإشتقاق على اليمين في 0 ج بين أن f تزايدية قطعا على 0 lim احسب أ 2 x f x ب بين أن 2 0 0 1 2 t t t e t 2 ج بين ان 4 4 2 x f 0 x x x x x gt د استنتج أن المنحنى C f يقبل مقاربا مائلا ينبغي تحديد معادلة له C f و المستقيم 3 أنشئ المنحنى الجزء الثاني n عدد صحيح طبيعي غير منعدم نعتبر الدالة العددية fn المعرفة على اجملال 0 بما يلي httpmathkasicima

3 2 2 0 0 0 x n n f x x e x n f gt f قابلة للإشتقاق على اليمين في 1 n 0 بين أن f على اجملال 2 n 0 ادرس تغيرات الدالة 2 nf x المعادلة 3 ا بين أن لكل n من تقبل حلا وحيدا an في اجملال n 0 ب بين أن 1 2 2 0 1 n n x n f x f x n n gt gt ج استنتج أن المتتالية an تناقصية ثم بين أن an متقاربة lim n نضع n a a د بين أن 2 2 2 n a n n n a e ه بين أن a 0 الجزء الثالث نعتبر الدالة العددية F المعرفة على اجملال 0 بما يلي 2 x x F x f t dt f هي الدالة المعرفة في الجزء الأول gt x 0 xf x Fx xf 2x أن بين أ1 x ب احسب lim F x 2 أ بين أن F قابلة للإشتقاق على اجملال 0 ب بين أن 2 1 1 2 1 3 2 0 0 0 x x x d F x e x e x e x F gt Fd 0 هو العدد المشتق للدالة F في0 على اليمين 3 أعط جدول التغيرات الدالة F التمرين الرابع 2 لكل عدد عقدي z مخالف للعدد 1 نصع 1 1 iz f z z 1 أ حدد العدد الحقيقي y بحيث f iy iy بحل في المعادلة E f z z httpmathkasicima

4 Re z z 1 2 gt Re و Re z0 0 حيث E المعادلة لحلول z2 و z1 و z0 ب نرمز 2أ تحقق أن 11 6 1 1 i z e و 7 6 2 1 i z e ب استنتج الكتابة المثلثية لكل من العددين z1 و z2 أن نفترض السؤال هذا في 3 i z e 0 lt حيث f z i zf z أن بين أ f z f z 0 أن علمت إذا حدد ب الشكل على f z اآتب ج i f z re حيث r 4 حدد z إذا علمت أن 1 1 2 z z Re انتهى httpmathkasicima

- 1 - تصحيح الإمتحان الوطني الموحد الأستاذ الحيان 2005 06 10 العادية الدورة الثانية بكالوريا علوم رياضية 2 2 2 2 ax by ay bx ab x y ab x y 1 1 2 Em m m m m ليكن 1 1 1 Xm m m m m و 1 1 Xn n n n n m n و عنصرين من المجموعة E إذن لدينا 1 1 11 Xm Xn m m n n m m nn 11 11 11 11 2 2 mn mn mn mn mn mn mn mn 1 11 1 2 2 mn mn mn mn mn mn mn mn n m mn n m mn n m mn n m mn 1 1 mn mn mn mn X m X n X mn أن وبما و m فإن n X m Xn E فإن وعليه mn X Y E XY E إذن قانون داخلي في المجموعة 2 E وبالتالي فإن 2 لدينا 1 1 E m mm m m m 6 أ ليكن i 2 لدينا m n 1 1 1 1 11 mn mn mn m m n n m n mn mn m m n n من تشاآل إذن E نحو 2 m n mn m n إذن X E ليكن ii 1 1 m Xm m m m نحو m Xm E وعليه فإن تقابل من ومنه نحو E وبالتالي فإن تشاآل تقابلي من زمرة تبادلية فإن E زمرة تبادلية نحو E وأن ب بما أن تشاآل تقابلي من ومنه فإن العنصر المحايد بالنسبة للقانون في E هو 1 20 لدينا 1 هو العنصر المحايد بالنسبة للقانون في ليكن 1 1 mm m m m عنصرا من E مماثل m بالنسبة للقانون في E هو 1 1 1 11 1 1 1 1 1 m m mm mm m m m m m 1 m 0 0 m المجموعة نعتبر 3 2 2 و y x 4 2 F xy x 2 التمرين 1

- 2 - نضع أ 1 1 2 Gm m m 0 m m لنبين أن F G lt ليكن G F 1 1 X mm G m m إذن m gt 0 لدينا 2 2 2 2 2 2 1 1 11 mm m m 4242 m m mm 2 تذآير 2 a b a b ab تطبيق 1 11 m mm 2 2 m mm وبناءا على ما سبق نجد X F ومنه نستنتج أن G F و x 2 إذن x y F ليكن F G 2 2 بحيث m gt 0 عن نبحث y x 4 1 1 xy m m m m 1 2 1 1 2 2 1 2 x y m x mxy m m xy m m m m x y m y m m m x y x y لأن أن ونعلم 22 22 2 4 4 4 2 x y y x x y x yx y x y 2 من أجل x y m لدينا 1 1 xy m m m m لنبين أن m gt 0 إذن x gt 2 0 ولدينا الإشارة نفس لهما x y و x y إذن 4 0 x yx y gt لدينا 0 فإن ومنه y y xyx xy 00 0 0 gt gt و y xyx gt 0 0 2 x y m gt F G نجد ومنه x y G إذن وبالتالي فإن F G i لدينا ب 1 1 2 Fm m m E 0 m m gt 20F لدينا m 1 أجل من لأن F ii ليكن iii 1 1 Xm m m m و 1 1 Yn n n n عنصرين من المجموعة F إذن 1 m m nm n XY m n m n n n mn m و m m n n gt gt gt X Y F فإن ومنه 2 X Y F XY F وبالتالي فإن F زمرة جزئية من E p I عدد صحيح طبيعي أولي و p 5 ومنه بينهما فيما أوليان p و 3 3 1 p إذن أولي 3 و p 5و أولي p لدينا 1 2 p 0 3 فإن وعليه 3 1 p ومنه نستنتج أن p 1 3 أو p 2 3 ندرس هاتين الحالتين فإن p 1 3 آان إذا i 2 فإن p 2 3 آان إذا ii p 1 3 2 إذن p 4 3 2 p 1 3 فإن وبالتالي 2 p 1 3 2 أ لدينا p عدد صحيح طبيعي أولي و p 5 إذن p عدد فردي ومنه q pq 21 ومنه 2 22 إذن p q q q qq 2 1 4 4 1 4 1 1 2 p qq 1 4 1 ب لدينا q وq 1 عددان صحيحان طبيعيان متتابعان إذن q q 1 عدد صحيح طبيعي زوجي ومنه التمرين 2

- 3 - إذن k qq k 1 2 2 نجد ومنه p 1 8k 2 p 1 8 3 خاصية a و b و c أعداد نسبية لدينا 1 a c b c ab c a b و b c n c bn و a c m c am لدينا برهان 2 1 1 Bezout a b u v au bv ab c أن نستنتج ومنه c cau cbv bnau ambv ab nu mv إذن ملاحظة الخاصية ليست صحيحة إذا آان a b 1 مثال مضاد 2 يقسم 12 و 4 يقسم12 لكن 8 24 لا يقسم 12 242 لدينا تطبيق 2 و p 1 3 2 إذن p 1 8 2 و 3 1 p 2 إذن 381 و 8 1 p 2 أي 24 3 8 1 p 2 p 1 24 II ليكن a عددا صحيحا طبيعيا حيث a 24 1 1 أ لديناa 24 1 إذن a عدد صحيح طبيعي فردي لو آان a زوجيا لكان 2 قاسما مشترآا ل a و 24 وهذا يتناقض معa 24 1 a 1 8 اتبع نفس خطوات السؤالين 2- I- أ و2- I- ب 2 ومنه نستنتج أن a 24 1مع يتناقض وهذا 24و a ل مشترآا قاسما 3 لكان a 0 3 آان لو a 0 3 إذن a 24 1ولدينا إذن a 2 3 أو a 1 3 إذن 2 و a a 13 13 2 2 aa a 23 43 13 لدينا 2 و a 1 8 2 إذن 381 و a 1 3 2 a 1 24 طبيعية صحيحة أعداد توجد أنه نفترض ب 1 و a 2 و و a 23 1 23 24 1 حيث a k k a و 22 2 1 2 23 aa a 23997 1 23 24 1 لدينا k إذن k a 2 123 1 24 k فإن ومنه k a 22 2 1 2 23 aa a 23 24 تناقض وهذا 2 0 24 أي 23 21 24 إذن 23997 21 24 ولدينا طبيعية صحيحة أعداد توجد لا خلاصة 1 و a 2 و و a 23 1 23 24 1 حيث a k k a و 22 2 1 2 23 aa a 23997 I نعتبر f الدالة العددية المعرفة على المجال 0 بما يلي 2 2 0 0 0 x fx x e x f gt الوحدة G JG 2cm منحناها في معلم متعامد ممنظم Cf Oi j وليكن نضع أ 1 2 X x x X 0 إذن ومنه 2 0 0 2 lim lim 2 lim 2 0 0 x X x x X fx x e e f X lim 0 لأن X X وبالتالي فإن f متصلة على اليمين في النقطة e 0 2 X ب نضع x x X 0 إذن ومنه 2 0 0 0 2 lim lim lim 1 lim 0 x X XX x x X X fx f x e X e e Xe x x lim 0 لأن X X X e lim 0و X X e 0 0 d f إذن f قابلة للإشتقاق على اليمين في 0 ولدينا ج ليكن x 0 لدينا 2 22 2 2 2 2 2 2 2 1 3 2 2 2 1 2 0 xx x x x x f x xe x e x e x e e xx x gt إذن f تزايدية قطعا على المجال 0 نضع أ 2 2 X x x X 0 إذن ومنه 2 lim lim 2 lim 2 2 X x x x X e fx x e X X التمرين 3
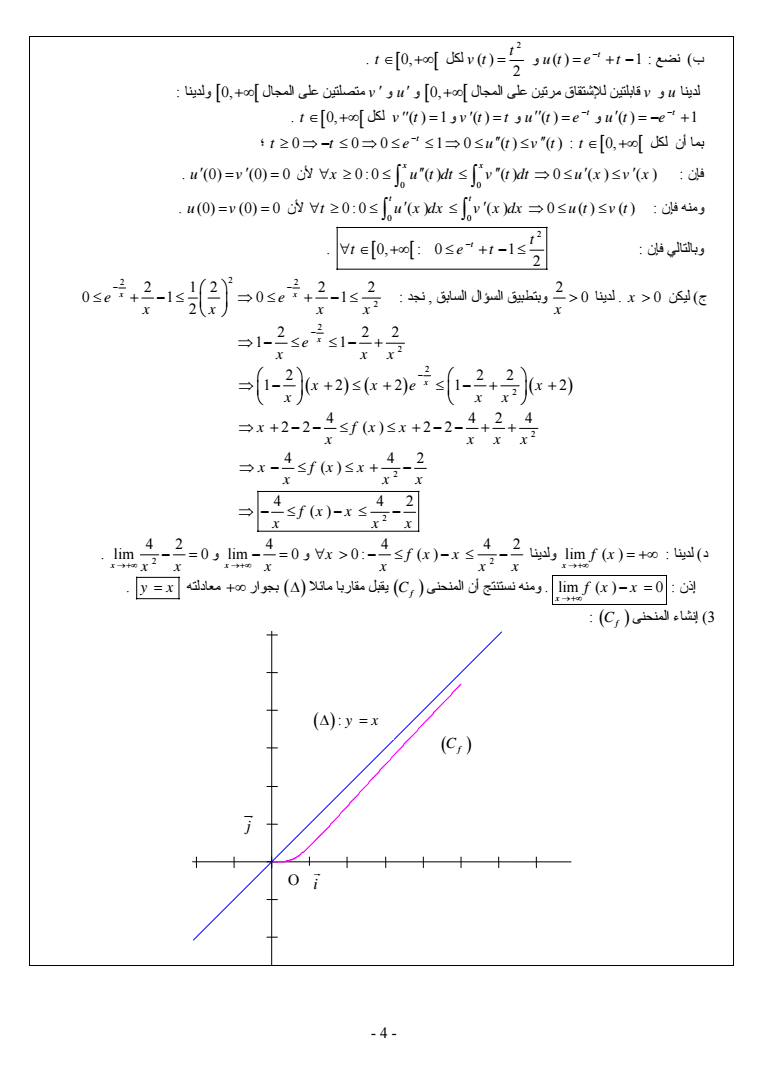
- 4 - 1 نضع ب t ut e t و 2 2 t t 0 لكل v t لدينا u و v قابلتين للإشتقاق مرتين على المجال 0 و u و v متصلتين على المجال 0 ولدينا 1 t ut e و t ut e t 0 لكل v t 1 و vt t و 0 0 0 1 0 t 0 لكل أن بما t t t e ut vt فإن 0 0 00 0 x x x u t dt v t dt u x v x u v 0 0 0 لأن فإن ومنه 0 0 00 0 t t t u x dx v x dx u t v t u v 0 0 0 لأن وبالتالي فإن 2 0 0 1 2 t t t et لدينا x gt 0 ليكن ج 2 0 x lt وبتطبيق السؤال السابق نجد 2 2 2 2 2 12 2 2 01 01 2 x x e e x x xx 2 2 2 22 1 1 x e x x x 2 2 2 22 1 221 2 x x xe x x xx 2 4 42 4 x fx x 2 2 2 2 x xxx 2 4 42 x fx x x x x 2 4 42 fx x x x x x د لدينا lim f x 2 ولدينا 4 42 x fx x 0 x x x و gt 4 lim 0 x x 2 و 4 2 lim 0 x x x lim 0 إذن x يقبل مقاربا بجوار معادلته Cf y x مائلا ومنه نستنتج أن المنحنى fx x 3 Cf إنشاء المنحنى Cf y x O i G j JG

- 5 - n و f n الدالة العددية المعرفة على المجال 0 بما يلي II ليكن 2 2 0 0 0 x n n fx x e x n f gt نضع 1 2 X x ومنه فإن إذن x X 0 2 0 0 0 2 1 lim lim 1 lim 1 lim 0 n n x X XX x x X X fx f X e e e Xe x nx n n lim 0 لأن X X Xe إذن n 0 0 ولدينا 0 في اليمين على للإشتقاق قابلة f n d f لدينا x gt 0 ليكن 2 22 2 2 2 2 2 2 2 22 1 0 xx x x n f x xe x ex e x e n n n x nx gt f دالة تزايدية قطعا على المجال n 0 إذن f n f تقابل من المجال 0 نحو المجال f n 0 0 متصلة وتزايدية قطعا على المجال 0 إذن 3 n أ لدينا 2 0 وبما أن فإن n 2 0 n nn a fa n n لدينا ب ليكن x gt 0 و 22 2 1 2 2 2 2 2 2 22 1 1 11 1 xx x n n f x fx x e x e e n n n n n nn n إذن 2 1 2 22 1 1 1 x n n f x fx e n n nn ومنه فإن 2 2 2 2 0 0 1 10 1 x x xe e x nn gt lt lt gt وبالتالي فإن 1 2 2 0 1 n n x n f x fx n n gt gt لأن لدينا ج 1 1 0 n n f a 11 1 1 22 2 0 1 n n nn nn f a fa fa nn n gt gt 1 2 n n f a n lt لأن n 0 نحو 0 من تقابل f 1 1 2 n n a f n lt لأن 2 n n f a n lt a a n n 1 n a gt n فإنها متقاربة نضع 0 n lim n متتالية تناقصية وبما أنها مصغورة بالعدد n n a 0 وبالتالي فإن a a د لدينا 2 2 22 2 2 2 22 22 2 2 n a n nn nn n n n n f a a e a e na e na e n n n nn لدينا ه 0 n lim 0 n إذن gt n a n a a نفترض أن a 0 إذن a gt 0 ولدينا 2 22 n a n lim n و n na e n na لكن 2 2 lim 2 2 2 2 n a a n e e وهذا تناقض وبالتالي فإن lim 0 n n a III نعتبر الدالة العددية F المعرفة على المجال 0 بمايلي 2 0 x x x F x f t dt 1 أ ليكن x gt 0 لدينا f تزايدية قطعا على المجال 0 و x 2x إذن

- 6 - إذن t x x x t x fx ft f x 2 2 2 22 2 2 xx x xx x f x dt f t dt f x dt x gt 0 لكل xf x F x xf x 2 فإن ومنه lim lim ولدينا x gt 0 F x xf x لدينا ب x x f x xf x x ومنه نستنتج أن lim F x 2 أ لدينا f متصلة على المجال 0 لتكن دالة أصلية للدالة f على المجال 0 إذن 2 0 2 x x x F x f t dt x x بما أن x 6 2x قابلة للإشتقاق على المجال 0 وتحول المجال 0 نحو المجال 0 وبما أن قابلة للإشتقاق على المجال 0 فإن x 6 2 x قابلة للإشتقاق على المجال 0 وبالتالي فإن F قابلة للإشتقاق على المجال 0 ولدينا 0 2 0 2 F x x xf x F x xf x x f x f x x و lt lt lim 0 x f x و lim 2 0 x f x فإن 0 0 0 lim lim 0 x x 0 Fx F Fx x x Fd إذن F قابلة للإشتقاق على اليمين في 0 و 0 0 وبالتالي فإن F قابلة للإشتقاق على المجال 0 ليكن x gt 0 لدينا Fd ب حسب أ نعلم أن 0 0 1 2 2 2 2 2 2 2 2 2 2 Fx x x x x x f x fx x e x e x x 21 2 1 1 1 4 1 2 2 1 2 4 1 Fx e x e x e x e x e x e xx x x x x ومنه فإن 21 1 2 1 3 2 Fx e x e x e xx x وبالتالي فإن 21 1 2 1 3 2 0 0 0 xx x d Fx e x e x e x F gt 3 لدينا 1 1 1 0 0 1 10 x x x ee lt lt lt lt و x 1 32 0 x x x gt gt 0 20 و x e gt إذن x Fx gt gt 0 0 ومنه فإن F تزايدية قطعا على المجال 0 جدول تغيرات الدالة F على المجال 0 x 0 F x 0 F x 2 1 1 1 iz z fz z 1 أ ليكن y عددا حقيقيا لدينا 2 2 2 2 2 1 1 1 12 1 2 1 1 2 1 1 0 y f iy iy iy iy y iy y iy y y iy y y y yy y التمرين 4

- 7 - 2 2 10 01 1 1 y y y yy y ب لدينا 2 2 3 2 3 2 1 1 1 2 1 1 2 2 1 1 0 iz f zz z z iz z z z iz z z z z z iz ل الأقليدية القسمة ننجز للمعادلة حل i إذن f i i أن نعلم 3 2 آمايلي z i على z z iz 2 1 1 z i 3 2 z z iz 2 1 1 3 2 z iz 2 z iz i 2 2 2 1 1 iz iz 2 2 1 2 iz iz iz 1 iz 1 00 إذن 2 2 2 0 2 0 f z z z i z iz i z i z iz i لدينا المعادلة نحل 2 2 هما حلين للمعادلة إذن 2 4 7 1 4 4 3 3 i i ii 2 3 3 1 1 2 22 i z i أو 2 3 3 1 1 2 22 i z i هي في f z z المعادلة حلول مجموعة فإن وبالتالي 31 31 1 1 22 22 Si i i أن بما 0 فإن R e z0 0 1 فإن Rez ez 1 2 gt R وبماأن z i 3 1 1 2 2 2 و z i 3 1 1 2 2 z i 2 أ لدينا 11 6 1 3 1 11 1 cos sin 1 1 2 1 22 6 6 6 6 6 i z ii e و 7 6 2 31 7 1 cos sin 1 1 1 22 6 6 6 6 6 i z ii e ب لدينا 11 11 11 11 11 11 17 6 12 12 12 12 2 12 12 1 11 11 11 1 2 sin 2sin 2sin 12 12 12 i i i i i ii i z e e e e i e ee e و 7 7 7 7 7 7 13 6 12 12 12 12 2 12 12 2 77 7 1 2 sin 2sin 2sin 12 12 12 i i i i i ii i z e e e e i e ee e 2 لأن i e i ولدينا 7 32 12 6 2 sin sin sin cos cos sin 12 3 4 3 4 3 4 2 2 2 2 4 11 3 2 1 2 6 2 sin sin sin sin sin cos cos sin 12 12 12 3 4 3 4 3 4 2 2 2 2 4
- 8 - ومنه نجد 17 17 12 12 1 62 62 2 4 2 i i ze e و 13 13 12 12 2 62 62 2 4 2 i i ze e نضع 3 i z e 0 lt حيث 1 أ لدينا z zz z 1 1 z إذن 22 2 2 2 22 2 1 1 1 1 1 1 iz i z iz z z iz z i z f z z z z z z zz z 2 ومنه 1 1 iz f z iz izf z z ب لدينا 2 1 0 0 0 1 0 1 0 0 1 z i iz z i f z f z izf z f z iz f z iz f z zi z 0 lt لأن إذن 2 2 0 2 2 2 i i e i f z fz e i ج لدينا 11 1 22 22 22 2 22 2 22 2 1 1 1 2cos 2 ii i i i i i i ii i i ee e ie e e f z fe e ee e e 1 1 3 2 22 22 4 22 2 1 2 sin sin sin 2 2 1 1 42 42 2 2 4cos cos cos 22 2 ii i i i f ze e e 0 0 sin 0 لأن وذلك 22 4242 42 و lt gt gt gt 0 0 cos 0 22 2 lt lt gt 4 لدينا 1 0 2 1 1 2 2 i z z e ef z ef z lt R R ولدينا 2 2 sin 1 32 1 32 4 2 cos sin cos cos 2 4 2 42 4 2 2cos 2 ef z R 12 2 2 cos sin cos sin cos 2 2 2 22 2 2 2 ef z R 11 1 22 2 2 cos sin cos cos cos 22 2 2 2 2 2 ef z R

- 9 - 2 22 2 11 1 1 2 3 2cos 1 cos cos cos 2 2 2 2 24 2 2 2 2 2 3 ef z R 2 4 1 3 2 4 4 3 ef z R ولدينا 2 3 2 13 4 3 22 i i ze e i j و 2 3 2 13 4 3 22 i i ze e i j و 4 2 3 3 4 4 3 i i i ze e e j و 4 2 3 3 4 4 3 i i i ze e e j وبالتالي فإن 2 3 1 3 2 2 i zj i e أو 2 3 1 3 2 2 i zj i e S jj طريقة أخرى لنحل النظمة التالية 1 1 2 z ef z R لديناz 1 إذن حسب السؤال 3- أ - لدينا f z izf z ومنه نستنتج أن 2 2 2 2 2 2 2 4 3 3 2 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 21 2 2 20 1 0 13 13 22 22 i i ef z f z f z ef z f z izf z iz f z iz iz z iz iz z z zz z z z z ze ze zj i zj j i R R وبالتالي فإن S jj طريقة أخرى لإنجاز السؤال 1 I من التمرين الثاني نضع 2 ومنه 3 m إذن متتابعة أعداد ثلاثة جداء هو m إذن m pp p 1 1 لدينا m pp 1 2 3 1 p p p 3 1 إذن p يقسم لا 3 و p gt 3 فإن p 5 و أولي p أن وبما وعليه فإن 2 2 3 1 3 1 3 1 p p Gauss p p وهذا يعني أن 2 p 1 3 طريقة أخرى لإنجاز السؤال 1 II من التمرين الثاني a و a 24 1 لدينا 1 2 لنفكك a إلى جداء عوامل أولية 1 2 r r a pp p r و و 2 و 1 و أولية طبيعية صحيحة أعداد pr و و p2 و p1 حيث
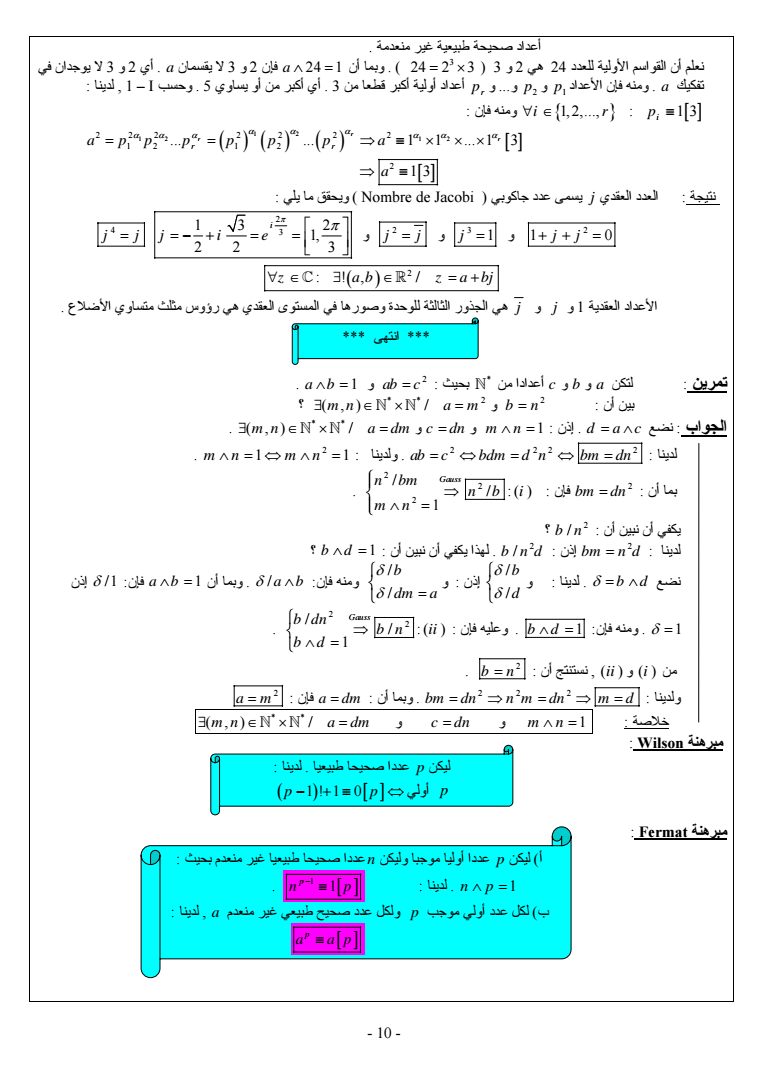
- 10 - أعداد صحيحة طبيعية غير منعدمة 24 2 3 وبما أن a 24 1 فإن 2 و 3 لا يقسمان a أي 2 و 3 لا يوجدان في 3 نعلم أن القواسم الأولية للعدد 24 هي 2 و 3 p أعداد أولية أآبر قطعا من 3 أي أآبر من أو يساوي 5 وحسب 1 I لدينا p r و و p 2 و 1 تفكيك a ومنه فإن الأعداد 1 2 1 3 i فإن ومنه i rp 1 2 1 2 1 2 2 22 2 2 2 2 12 1 2 1 1 1 3 r r r r r a pp p p p p a 2 a 1 3 نتيجة العدد العقدي j يسمى عدد جاآوبي Nombre de Jacobi ويحقق ما يلي 2 و 1 0 j j 3 و j 1 2 و j j 2 3 13 2 1 22 3 i j ie 4 j j 2 z a b z a bj الأعداد العقدية 1 و j و j هي الجذور الثالثة للوحدة وصورها في المستوى العقدي هي رؤوس مثلث متساوي الأضلاع من أعدادا c و b و a لتكن تمرين بحيث 2 a b 1 و ab c 2 بين أن و b n 2 mn a m و c dn و m n 1 إذن d ac نضع الجواب m n a dm لدينا 2 22 2 ولدينا ab c bdm d n bm dn 2 mn mn 1 1 bm dn فإن 2 بما أن 2 2 2 1 n bm Gauss nb i m n b n 2 يكفي أن نبين أن لدينا 2 إذن bm n d 2 b d 1 أن نبين أن يكفي لهذا b nd نضع b d لدينا و b d إذن و b dm a إذن 1 فإن a b 1 أن وبما a b فإن ومنه فإن وعليه b d 1 فإن ومنه 1 2 2 1 b dn Gauss b n ii b d أن نستنتج ii و i من 2 b n ولدينا 22 2 فإن a dm أن وبما bm dn n m dn m d 2 a m و c dn و m n 1 خلاصة m n a dm مبرهنة Wilson مبرهنة Fermat انتهى ليكن p عددا صحيحا طبيعيا لدينا p p 1 1 0 أولي p أ ليكن p عددا أوليا موجبا وليكن n عددا صحيحا طبيعيا غير منعدم بحيث 1 1 p n p لدينا n p 1 ب لكل عدد أولي موجب p ولكل عدد صحيح طبيعي غير منعدم a لدينا p a ap

- 1 - 1 2 2 Ex y 1 95 E x y 2 2 2 2 1 95 1 4 5 1 40 5 1 40 5 12 12 0 5 1 305 xy x x x x x x x 5 1 x 5 3 x x 1 5 x 3 5 x 1 5 x 2 5 2 E x 2 5 x 1 5 E x y 2 2 2 2 1 5 15 25 95 125 4 20 25 9 5 5 5 20 25 14 5 x k xk k k yx k k kk y k y kk k y kk 2 2 2 2 2 5 25 35 95 135 9 30 25 9 5 5 30 25 65 x k xk k k yx k k kk y k ykk k y kk 2 151 4 5 k kk 2 E k 2 5 6 5 kk k 2 2 S k k k kk k k 1 5 1 4 5 2 5 6 5 k 2 5 1 k 2 5 41 k k 2 e 5k k 2 5 41 51 31 k k kk k k 3 1 k 2 2 5 4151 5 41 51 51 k k k k k kk k 31 51 k k

- 2 - 2 31 5131 31 2 2 312 2 2 2 322 3 2 22 3 5 1 5 1 38 k kk k k kk k k k k kk kk k k 2 k kk k k 5 4 1 5 1 38 3 2 121 59 8 1 5 x y x y x 2 2 2 2 2 2 2 21 5 9 8 1 5 1 95 8 1 5 1 5 1 4 5 2 5 6 5 8 1 5 151 4 5 15 14 5 8 1 5 151 4 5 38 8 1 5 xx y x y x x y x y x x y k k k ou x y k k k k x y x xy k k k k k kk x xy k k k k k x 2 151 4 5 8 3 1 5 xy k k k k k x 2 151 4 5 38 xy k k k k h kh 1 3 0 15 0 0 38 0 0 5 8 x x k k k hh hh 2 1 53 8 1 43 8 53 8 xy h h h h 2 16 40 56 272 320 xy h h h h

- 3 - 2 2 S h h hh 16 40 56 272 320 2 2 1 210 10 2 m x y C m m m 10 0 10 gt lt m m 20 2 gt lt m m 1 I 2 0 gt m m lt 2 2 2 2 2 1 10 2 m x y C m m C m 10 0 gt m 2 0 lt m 2 10 lt lt m 2 2 2 2 1 10 2 m x y C m m C m 2 0 lt m 10 0 lt m m gt10 2 2 2 2 1 0 10 2 x y m m lt C m m lt 2 2 2 2 2 2 1 m x y C a b a b gt b m 2 a m 10 C m O 10 m A 10 m A 2 B m 2 B m 2 2 c ba m m 10 2 8 2 2 C m 2 2 F 2 2 F 2 10 lt lt m 2 2 2 2 1 m x y C a b b m 2 a m 10 C m O 10 m A 10 m A 2 2 c ab m m 2 10 8 2 2 C m 2 2 F 2 2 F 2 10 b m Dy x y x a m 2 10 b m Dy x y x a m 3 C1 4 2 2 F 2 2 F A A B B
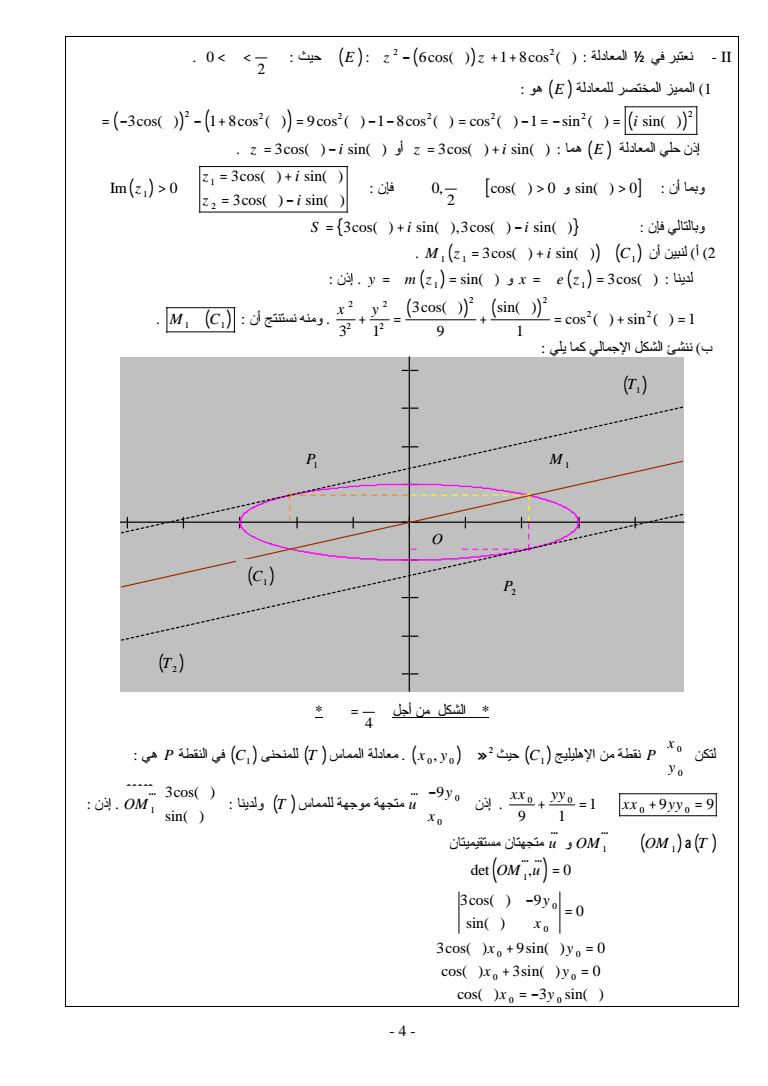
- 4 - - II 2 2 0 Ez z 6cos 1 8cos 2 lt lt E 1 2 2 2 2 22 2 3cos 1 8cos 9cos 1 8cos cos 1 sin sin i z i 3cos sin z i 3cos sin E 0 cos 0 sin 0 gt 2 gt 1 1 2 3cos sin Im 0 3cos sin z i z z i gt Si i 3cos sin 3cos sin 2 11 1 Mz i C 3cos sin 1 x ez R 3cos 1 y mz I sin 2 2 2 2 2 2 2 2 3cos sin cos sin 1 31 9 1 x y M C 1 1 4 x P y C1 2 0 0 P C1 T x y 0 0 0 0 1 99 9 1 xx yy xx yy 9y u x r T 1 3cos sin OM uuuuur OM T 1 P OM 1 uuuuur u r 1 0 0 0 0 det 0 3cos 9 sin 3cos 9sin 0 cos 3sin 0 OM u y x x y x y uuuuur r 0 0 cos 3 sin x y C1 P1 P2 O M 1 T1 T2

- 5 - 0 0 sin 3 cos x y 2 2 0 0 0 1 2 2 2 2 0 0 2 2 2 0 0 00 2 22 22 2 0 0 00 2 2 0 00 0 00 1 3 1 9 9 sin sin 9 9 9 3 cos cos sin sin cos cos 3 cos sin cos 3 cos sin cos 3 cos x x y P C y x y y y xy y y xy y xy y xy m3sin 1 3sin cos P 2 3sin cos P 1 3sin cos P 2 3sin cos P C1 C1 T2 T1 T xy 1 3sin 9cos 9 0 OM 1 2 Txy 3sin 9cos 9 0 P C 1 1 P C 2 1 1 1 2 2 3sin sin 3cos 3 0 cos 3sin sin 3cos 3 0 cos P Txy P Tx y T T OM 12 1 P P OM i 1 3cos sin uuuuur 2 OM i 3cos sin uuuuur 1 OP i 3sin cos uuur 2 OP i 3sin cos uuur 22 2 2 2 2 2 2 1 1 OM OP 9cos sin 9sin cos 10 cos sin 10 22 2 2 2 2 2 2 2 2 OM OP 9cos sin 9sin cos 10 cos sin 10 22 22 OM OP OM OP 11 22 n 20 n N B 0 k n n k k p n 10 10

- 6 - 1 1 1 10 10 1 1 10 10 1 1 k nk k nk k k kn n n n C C pC C C C nn 10 10 k nk k k n n p C n n 2 1 01 1 k k k p k nu p 1 1 1 1 1 1 10 10 10 1 10 1 10 10 10 10 k nk k k n n k k n k k nk k k k n k n n n A C p C n n k u p Cn n n n A C n n n k 1 10 10 1 1 1 10 1 10 n n nk k nk n n nk k n k n 10 1 1 1 10 10 1 10 10 10 10 10 0 10 10 0 10 9 10 9 10 9 10 9 k n k u k n nk k n n k nk k n nk n n nk n n nk n k n n 1 1 10 1 20 20 2 n n n 1 1 9 2 k k u k 1 0 9 k iu k 10 1 1 10 10 10 10 10 9 10 9 10 10 9 10 1 k n k u k n n k nk n k n nk n nk k n k n k n 01 1 k 10 1 20 0 2 n n lt 1 10 1 k ii u k n 1 0 10 1 1 p u pp p 2 1 21 1 1 1 p u pp p M M M M M

- 7 - 10 9 10 9 9 1 1 p u pp p ip p p p p 10 9 2 1 0 11 10 11 10 10 1 1 p u pp p 12 11 12 11 11 1 1 p u pp p M M M M M M M M 1 1 1 1 1 n n nn n p u pp p ii p p p p p n n 1 12 11 10 ii i 01 2 k 10 k n pp M k 01 2n k p 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 n n n n n n n n n nn Mp C nn n nn n n 2 1 x x f x xe 1 I 2 22 lim lim 1 lim 0 0 0 x xx xx x f x x e e xe x t t x 2 2 1 lim lim 0 2 x t x t xe te x t t x 2 2 1 lim lim 1 lim 1 2 x t xx t f x xe t e lim 0 x f x y 0 C lim - x f x 2 1 2 lim lim 1 lim 1 x t xx t f x e e xx t 2 x t x C x 2 2 2 22 1 1 2 1 21 1 2 x x xx f x x e x e x e xe f 1 2 x f x 1 2 x f x 0 - 1 2 e f x x 3 2 2 22 1 2 1 2 2 2 21 2 4 x x xx f x x e x e x e xe x 0 f x - 0 C 1 A C C A01 C
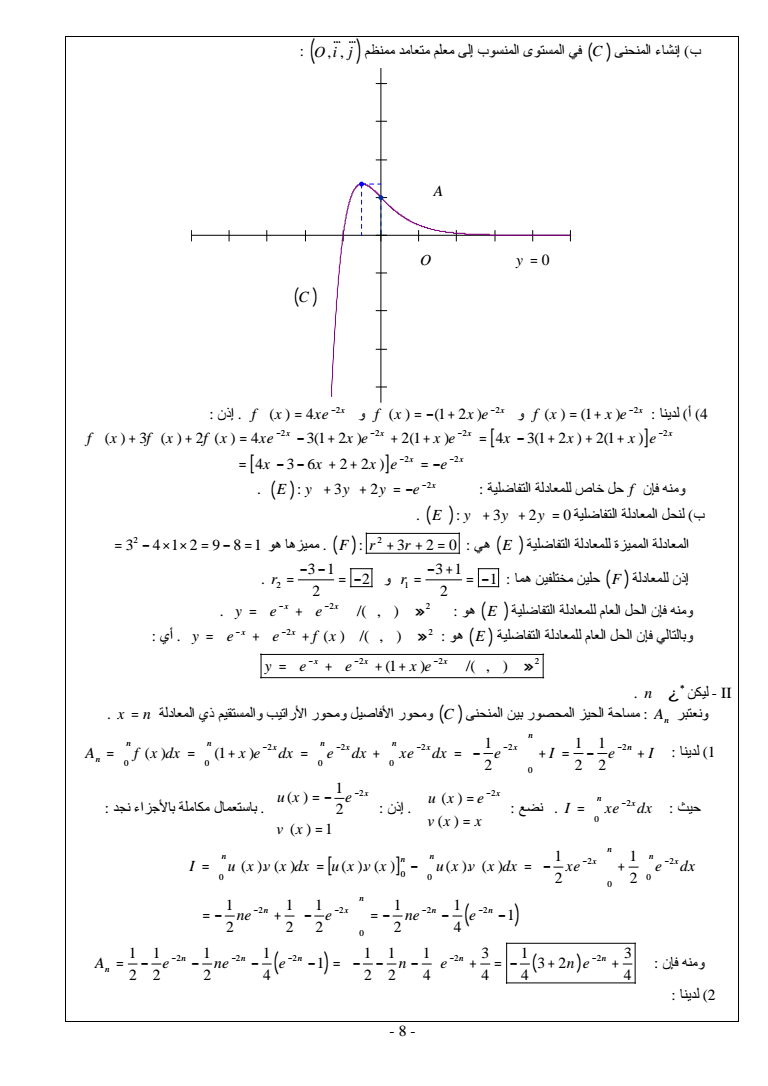
- 8 - Oi j C r ur 4 2 1 x f x xe 2 1 2 x f x xe 2 4 x f x xe 2 22 2 3 2 4 31 2 21 4 31 2 21 x xx x f x f x f x xe x e x e x x x e 2 2 4 3 6 2 2 x x x x xe e f 2 32 x Ey y y e Ey y y 320 E 2 Fr r 3 20 2 3 412 9 8 1 F 1 3 1 1 2 r 2 3 1 2 2 r E 2 2 x x ye e E 2 2 x x y e e fx 22 2 1 xx x y e e xe - II n An x n C 1 22 2 2 2 0 0 00 1 11 1 2 22 n n n nn xx x x n A f x dx x e dx e dx xe dx e I e I n 2 n x I xe dx 2 x ux e vx x 1 2 2 1 x ux e v x 2 2 0 00 0 1 1 2 2 n nn n n x x I u x v x dx u x v x u x v x dx xe e dx 2 2 22 1 11 1 1 1 2 22 2 4 n n x nn ne e ne e 11 1 1 11 1 3 1 3 2 22 2 2 1 32 22 2 4 22 4 4 4 4 n nn n n A e ne e n e n e n 2 C O y 0 A

- 9 - 1 3 13 3 2 lim lim 3 2 lim 4 44 4 n n m nn m m A ne e 2 m n n 13 1 33 lim lim 4 44 n m m n m A e e m 3 lim 4 n n A ua III 1 n n n u n f x dx dt ndx x tn 1 x t 0 0 t nx 1 2 2 00 0 1 1 n n t n nn n n t n tt t u f dt e dt e dt nn n 1 2 u u 1 2 2 1 1 u 2 2 1 1 2 1 2 0 uu u u u uu 1 2 u u 1 u u 12 2 1 u 1 u u 12 2 1 u u t 12 01 u t 1 t u 1 1 01 2 1 1 1 t t t 1 01 1 1 1 t t t 2 0 00 0 1 01 1 01 ln 1 0 1 2 u u uu t u u t dt dt dt u t t u t 2 01 ln 1 2 u u u uu x u n 01 x n 0 x u n 2 ln 1 2 u u uu 2 ln 1 2 xx x x nn nn 2 2 0 ln 1 2 x x n x nx n x n n 3 n 2 1 n n t n t u e dt n t n 0 2 2 0 0 ln 1 ln 1 1 1 1 n n t n t t n n n t t n t n t t nt t n n t e n t e e n t e dt e dt n u e dt n x n n u e dx n

- 10 - 2 2 2 2 2 2 2 2 ln 1 1 2 1 t n t n t n t n t t n t n n tt t tn e nn n t e e n e dt u 2 3 3 n n nnn n 1 1 2 2 0 0 t t n t ne 2 2 3 2 2 0 0 t t n n t t n n e dt e dt 2 3 2 3 2 3 3 3 2 2 3 3 3 3 2 2 3 3 2 2 2 3 1 2 2 1 2 2 1 2 2 0 0 1 2 2 2 00 0 0 0 1 2 2 1 t n n t t t n n t n n t t n n t t nn n t t n t n n n tn t n n t t n n e e e e e dt e dt e e dt e dt e dt u 3 3 1 2 0 0 n n n x x n n e e dx u e dx 0 0 1 n n xx n e dx e e 3 3 3 0 0 1 n n xx n e dx e e 3 3 1 2 1 1 n n n n n e eue lim 1 1 n n e 3 3 1 2 lim 1 1 n n n e e n lim 1 u n n u a 01 4 0 f 2 f e 1 2 0 1 1 1 1 1 1 1 n n n n a a n n a x a a x f fx fa fx fa n f x dx n f a dx n f x dx n a f a 1 0 1 n n a n n f x dx n a f a ln lim 1 lim 1 n n fa n n n a f a a ne 2 0 1 1 0 0 2 1 ln 0 a f fa f e fa fa lt lt lt lt lt lt lt lt 1 1 ln lim 1 lim ln lim 0 ln ln n n fa x nn x a a n a f a n f a e xe fa fa

- 11 - ln 0 f a lt x n fa ln n x lim 0 0 n 1 lim 0 n n a n f x dx 1 1 lim 1 lim 1 lim 1 lim 1 n n n n a n n n a a n n u n f x dx n f x dx n f x dx n f x dx 1 lim 0 n n a n f x dx 01 lim 1 a n n a n f x dx

13 الصفحة مدة الإنجاز 4 ساعات الامتحان الوطني الموحد لنيل شهادة البكالوريا الدورة العادية يونيو 2004 المملكة المغربية وزارة التربية الوطنية والشباب المعامل 10 المادة الرياضيات الشعبة علوم رياضيةأ وب يسمح باستعمال حاسبة غير قابلة للبرمجة التمرين3 1نقط 1- ليكن n عددا صحيحا طبيعيا 2 n 1 8 أ بين أ نه اذا آان n فرديا فان ب بين أ نه اذا آان n زوجيا فان 2 أو n 0 8 2 n 4 8 2- ليكن a و b و c أعدادا صحيحة طبيعية فردية abc ليس مربعا آاملا أي ليس مربع للعدد صحبح طبيعي 222 أ بين أن 2 68 ab bc ac أن بين ب ملاحظة يمكن 2 222 a b c a b c ab abc ac 2 2 ج استنتج أن 2ab bc ac ليس مربعا آاملا د بين أن ab bc ac ليس مربعا آاملا التمرين3 2نقط لتكن E مجموعة المصفوفات التي تكتب على شكل 1 1 3 1 0 a a a a M a و F مجموعة المصفوفات التي تكتب على شكل 1 1 3 3 a a a N a a a حيث a أن بين أ -1 2 ab M M M a b ab نحو E بحيث a M a ب ليكن التطبيق المعرف من نحو E بين أن تشاآل من استنتج البنية الجبرية ل E أن بين أ -2 2 a b b a a b N N M ب نضع GEF بين أن G زمرة ج هل G زمرة تبادلية ن 350 3التمرين المعادلة في حل -1 2 z z 1 1 cos sin حيث z عقدي عدد لكل -2 i ze i و مع 2 3 و 2 3 2 نضع 1 1 z z z أن تحقق أ 2 1 1 zz z zz

ب أجسب معبار وعمدة z بدلالة حيث z x iy نضع ج 2 x y أن بين 2 2 2 x y x 1 2 د استنتج أن النقطة M ذات اللحق z تنتمي الى هذلول يتم تحديد مرآزه و رأسيه و مقاربيه التمرين10 4نقط ب I نعتبر f الدالة المعرفة على x e f x x 1- أحسب نهايات f عند محدات مجموع تعريفها 2- أدرس تغيرات f 3- ليكن C المنحنى الممثل للدالة f في معلم متعامد ممنظم أ أدرس الفروع اللانهائية للمنحنى C ج أنشئ C u المتتالية العددية المعرفة ب II n لتكن 2 1 0 1 n u n u u f u ue u n n nn 1 أن بين -1 x x e x أن استنتج -2 2 0 1 x x xfx x 3 1 0- أ باستعمال البرهان بالترجع بين أن 1 n un n ب بين أن un متقاربة وحدد نهايتها 4- نضع من أجل آل n من 1 n n k k v u 1 ln n أ- بين أنه n n v u n v ب- حدد نهاية III نعتبر الدالة F المعرفة على 0 بما يلي 2 2 4 0 x x F x f t dt x F 0 2ln 2 و 1- أ تحقق أن 2 2 4 1 0 2ln 2 x x x dt t 0 10 أن بين 1 II نتيجة باستعمال ب t t te أن بين أ -2 2 x x Fx 0 3 2ln 2 0 ب استنتج أن F متصلة و قابلة للاشتقاق على اليمين في 0 1 أن بين أ -3 t t ft e x ب استنتج lim F x 4- أ بين أن أ F قابلة للاشتقاق على 0 و أحسب F x ب أعط جدول تغيرات F CF في معلم متعامد ممنظم ج أنشئ المنحنى 5 4- لتكن G الدالة المعرفة على 0 ب ln x t x G x e t dt 23 صفحة

أن بين أ 4 0 ln 4 ln x x x Gx F x e x e x ب أحسب 4 lim ln x x x ee x ت استنتج lim x G x 33 صفحة

Exercice 1 3 points 1 Congruence de n a n impair implique n2 congru 1 modulo 8 Soit n un entier impair Il existe donc un entier k tel que n k 2 1 do 1 2 2 n k 4 4 k 1 4kk 1 Si k est pair alors k 1 est impair et si k est impair alors k 1 est pair donc dans tous les cas k k 1 est pair cest dire quil existe un entier p tel que k k 1 2 p On en dduit alors que autrement dit 2 n 8p 1 2 n 1 8 Finalement si n est un entier naturel impair alors est congru un modulo huit 2 n b n pair implique n2 congru 0 ou 4 modulo 8 Soit n un entier pair Il existe alors un entier k tel que n 2k soit On distingue alors deux cas 2 2 n 4k gtgt Premier cas Si k est pair alors il existe un entier p tel que k 2 p do 2 2 2 2 n p 44 16 p n 0 8 gtgt Deuxime cas Si k est impair alors il existe un entier p tel que k 2 p 1 do 2 2 2 2 n p 42 1 16k 16k 4 16k k 4 Comme est divisible par 8 alors 2 16k k 2 n 4 8 Finalement si n est un entier naturel pair alors est congru zro ou quatre modulo huit 2 n 2 Un carr parfait a a2 b2 c2 nest pas un carr parfait a b et c sont trois entiers naturels impairs Daprs la question 1a on a et do 2 2 a 1 8 b 1 8 2 c 1 8 2 2 2 abc 3 8 Daprs la question 1 un carr parfait est congru zro un ou quatre modulo huit donc nest pas un carr parfait 2 2 2 a b c 2 2 2 a b c nest pas un carr parfait b 2abbcac est congru 6 modulo 8 On a 2 2 2 2 abc a b c 2ab ac bc 2

Do 2 2 2 2 abc a b c 2ab ac bc Comme a b et c sont trois entiers naturels impairs alors a b c est aussi impair Daprs la question 1a on a 2 abc 1 8 Daprs la question 2a on a 2 2 2 abc 3 8 Donc 2 2 2 2 a b c a b c 2ab ac bc 1 3 8 2 8 6 8 2ab ac bc est congru 6 modulo 8 c 2ab bc ac nest pas un carr parfait daprs la question 1 un carr parfait est congru soit zro soit quatre modulo huit comme 2ab ac bc 6 8 alors 2ab ac bc nest pas un carr parfait d ab bc ac nest pas un carr parfait Daprs la question 2b on a 2ab ac bc 6 8 donc il existe un entier naturel p tel que 2ab ac bc 8p 6 autrement dit ab ac bc 4 3 p Do ab ac bc 3 4 Montrons maintenant quun carr parfait est congru soit zro soit un modulo quatre Soit n un entier naturel gtgt Si n est impair alors il existe un entier tel que do k n k 2 1 n k k 1 n 1 4 k 2 2 2 4 4 gtgt Si n est pair alors il existe un entier k tel que n 2 do 2 2 2 n k 4 0 n 4 gtgt Conclusion Un carr parfait est congru soit zro soit un modulo quatre comme alors nest pas un carr parfait ab ac bc 3 4 ab ac bc 3

Exercice 2 3 points 1 Une structure algbrique a Produit de deux matrices Soient a et b deux rels non nuls on a 1 1 1 1 1 1 1 3 3 3 3 1 1 1 0 0 0 a b a a a b b ab b a a b b b M M a b ab a Or 1 1 1 1 1 1 1 3 3 3 3 a a a b a ab ab b b a b b ab ab do 1 1 3 1 0 a b a ab ab ab M M M b ab b est un morphisme est lapplication dfinie de dans par E a a M Montrer que est un morphisme de dans E revient montrer que ab a b On a ab a b ab M M M daprs la question prcdente donc ab a b c Structure algbrique de lensemble E Lapplication est bijective comme est un groupe multiplicatif alors est aussi un groupe multiplicatif E 2 Un groupe a Produit de deux matrices Soient a et b deux rels non nuls on a 1 1 1 1 1 1 3 3 3 3 1 3 3 3 3 a b a b ab b a b a a a b b a b N N a b a a b b ab ab a b ab b 1 a 4

do 1 3 a b a b b a a a b N N M a b b b G est un groupe 1 G est stable par la loi On a G E F et on propose de montrer que G muni de la multiplication est un groupe Soient x et y deux lments non nuls de G Si x et y sont dans E comme E est un groupe question 1c alors x y E produit de deux matrices 2x2 donne une matrice 2x2 et fortiori x y G Si x et y sont dans F alors il existe deux rels non nuls a et b tels que a x N et b y N et donc a b b a x y N N M F do x y G Si x est dans F et y est dans E alors il existe deux rels non nuls a et b tels que a x N et do b y M a b a ab a a ab a x y N M N M N N N daprs la question 2a Alors a a ab x y N N N le produit matriciel tant associatif Or a a a 1 a N N M M I2 avec Matrice identit 2 1 0 0 1 I Do 2 ab ab x y I N N F et fortiori x y G Si x est dans E et y est dans F alors il existe deux rels non nuls a et b tels que a x M et do b y N 1 2 a b b b b b b b b b b b b a a a b a a a x y M N N N N N N N N M N M N I N F donc x y G 2 G admet un lment neutre De plus 2 1 I M G et 2 2 2 2 a a a a a a M I I M M N I I N N 2 donc I est llment neutre de G 3 Les lments de G sont inversibles On a donc linverse de par la loi N N a a M 1 I2 Na est Na 1 2 N N a a I et est donc dans G 5

De mme a 1 a M M 2 I donc linverse de Ma par la loi est 1 a M et est donc dans G c Le groupe G est-il commutatif Soient et deux lments de G et soient et deux rels non nuls Na Nb a b Si le groupe G est commutatif alors N N a b Nb Na autrement dit b a a b M M Or en prenant a 1 et b 2 on a 2 2 1 3 2 2 3 1 0 2 M M et 1 2 1 3 2 2 3 0 2 M donc b a a b b a b M M N N N Na G nest pas un groupe commutatif 6

Exercice 3 3 points et 12 1 Rsolution dune quation Le discriminant du polynme et ngatif et vaut 2 z z 1 3 lquation admet donc deux racines complexes conjugus nots et avec 1 0 2 z z 1r 2 r 1 1 3 2 i r et 1 1 3 2 i r 2 Un ensemble de points a Une galit Soit z 0 On a 2 1 z z 1 1 z z z comme z a i b alors 2 1 a i b z z Or dans le cadre de cet exercice on a z 1 donc 1 a ib z z do lgalit 2 z z 1 z 1 z z b Le module et un argument de z On a 2 1 1 1 1 z z z z z z Comme i z e alors 1 i e z de plus on a z z 2cos do 1 1 1 1 1 1 1 2cos z z z z z z z et 1 1 1 1 arg arg arg arg arg 1 1 2cos z z z z z on distingue alors deux cas gtgt Premier cas 1 2 gt cos 0 alors 1 1 arg arg arg 1 2cos z z gtgt Deuxime cas 1 2 lt cos 0 alors 1 1 arg arg arg 1 2cos z z c Une galit On pose z x i y avec et on propose de montrer que 2 x y 2 2 2 x y 1 2x 7

On a 1 1 1 cos sin cos sin cos sin 1 1 2cos 1 2cos 1 2cos i i z i z z z Comme z x i y alors cos 1 2cos x et sin 1 2cos y Do 2 2 2 2 2 2 cos sin 1 1 2cos 1 2cos x y Il reste montrer que 2 2 1 1 2 1 2cos x - On a 2 2 2 2cos 1 1 2 1 1 2cos 1 2cos x CQFD Finalement 2 2 2 x y 1 2x d Lensemble des points M Le point M est le point daffixe il sagit de montrer que cet ensemble de points appartient une hyperbole que lon caractrisera z On a daprs la question prcdente soit 2 2 2 x y 1 2x 2 2 2 2 2 4 1 1 2 3 4 1 3 3 3 x y x x x x x 2 2 2 2 4 3 2 3 3 9 9 3 y x x 1 9 2 2 2 1 3 3 y x 9 2 2 2 9 3 3 x y 1 2 2 2 2 2 3 1 1 1 3 3 x y On reconnat alors lquation dune hyperbole dont le foyer est le point de coordonnes 2 0 3 de demi axe transverse 1 3 et de demi axe non transverse 1 3 8

Exercice 4 10 points et 12 I Etude de f est la fonction dfinie sur par x e f x x 1 Limites de aux bornes de son ensemble de dfinition gtgt Limite de f au voisinage de Dans un soucis de clart on pose y x on a alors lim lim lim lim x y y x x y y e e e f x x y y do lim x f x gtgt Limite de f gauche de zro 0 0 lim lim x x x e f x x comme lim 1 x x e et lim 0 x x Alors lim x f x gtgt Limite de f droite de zro 0 0 lim lim x x x e f x x comme lim 1 x x e et lim 0 x x alors lim x f x gtgt Limite de f au voisinage de 1 lim lim lim 0 x x x x x e f x x x e lim 0 x f x 2 Variations de gtgt Expression de la drive La fonction x x e 6 est drivable sur La fonction 1 x x 6 est galement drivable sur 9

Donc f est drivable sur et 2 2 1 x x x xe e e x f x x x x gtgt Signe de la drive Comme pour tout rel x dans et alors le signe de 2 x gt 0 0 x e gt f ne dpend que de celui de 1 x cest dire que sur f x lt 0 1 sur f x gt 0 1 et f 1 0 gtgt Tableau de variations x 1 0 f x - - f x 1 e 3 Branches infinies et construction de C a Nature des branches infinies de C gtgt Puisque alors la courbe admet laxe des abscisses comme asymptote horizontale au voisinage de linfini lim 0 x f x C gtgt Puisque alors la courbe C admet laxe des ordonnes comme asymptote verticale lim x f x gtgt Puisque alors la courbe C admet laxe des ordonnes comme asymptote verticale lim x f x gtgt Comme lim x f x il faut calculer lim x f x x On a 2 lim lim x x x f x e x x donc la courbe C admet au voisinage de linfini une branche parabolique 10
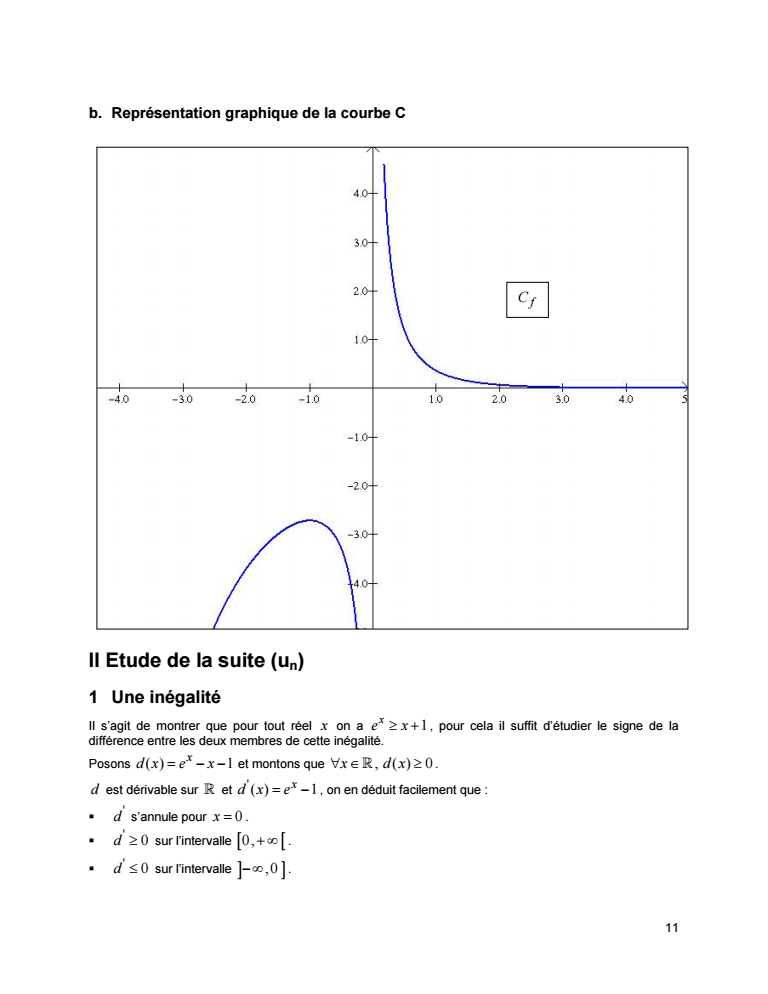
b Reprsentation graphique de la courbe C Cf II Etude de la suite un 1 Une ingalit Il sagit de montrer que pour tout rel x on a pour cela il suffit dtudier le signe de la diffrence entre les deux membres de cette ingalit 1 x e x Posons 1 et montons que x d x e x x d x 0 d est drivable sur et on en dduit facilement que 1 x d x e sannule pour d x 0 sur lintervalle d 0 0 sur lintervalle d 0 0 11

gtgt Do le tableau de variations de la fonction d x 0 d x - d x On voit daprs le tableau de variations ci-dessus que d admet un minima en x 0 et que d0 0 Conclusion Pour tout rel x on a 1 0 x d x e x do 1 x e x gtgt Nota On peut montrer cette ingalit de la manire suivante x 0 on a - 0 0 0 1 1 x x x x t t x x e e dt dt e x e x e x 1 2 Une autre ingalit On propose de montrer que pour tout rel x strictement positif on a 2 1 x xfx x pour cela et comme indiqu dans lnonc on utilise lingalit tablie la question prcdente cest dire 1 x e x 1 1 1 x e x pour tout x gt 0 1 1 x e x car 1 x x e e On divise les deux cts de cette ingalit par x pour faire apparatre lexpression de f x x tant strictement positif --gt division autorise pas de changement de sens pour lingalit Il vient 1 1 x e x x x gtx 0 On multiplie finalement les deux cts de cette ingalit par 2 x et on obtient 2 1 x x f x x 3 Limite de un a Encadrement de un Il sagit de prouver par rcurrence que pour tout entier naturel n on a 1 0 1 n u n lt gtgt 0 nu gt Pour n 0 on a donc la relation est vraie lordre zro 0u gt1 0 On suppose que la relation est vraie lordre n cest dire que u 0 et on sintresse lordre n gt n 1 12

On a daprs lhypothse de rcurrence on sait que de plus lexponentielle tant toujours positive on en dduit alors que La relation est vraie lordre Elle est donc hrditaire 1 n u n n u u e 0 nu gt n 0 u e gt 1 0 nu gt n 1 gtgt 1 1 nu n Pour n 0 on a et 0u 1 1 1 0 1 donc la relation est vraie lordre zro On suppose que la relation est vraie lordre n cest dire que 1 1 nu n et on sintresse lordre n 1 On a or nous avons montr 2 1 n n u u f u n la question prcdente que pour tout rel x strictement positif on a 2 1 x xfx x et comme 0 alors nu gt 2 1 n n n n u u f u u Daprs lhypothse de rcurrence on a 1 1 nu n de plus la fonction 1 x x x 6 est croissante sur 0 pas de changement de sens pour lingalit Lingalit 2 1 n n n n u u f u u devient alors 2 1 1 1 1 1 n n n u f u n 2 1 2 n n u f u n la relation est vraie lordre elle est donc hrditaire n 1 Finalement pour tout entier naturel n on a 1 0 1 n u n lt b Convergence et limite de la suite un On utilise lencadrement de dmontr nu la question prcdente cest dire 1 0 1 n u n lt et on passe la limite notons que le passage la limite fait changer les ingalits strictes en ingalits larges On a 1 0 lim lim 1 n n n u n comme 1 lim 0 n n 1 alors daprs le thorme des gendarmes on a lim 0 n n u La suite est donc convergente et sa limite vaut zro nu 13

4 Etude de la suite vn a Une autre expression de vn La suite est dfinie pour tout entier naturel n non nul par nv 1 n n k v k u on propose de montrer que 1 ln n n v u On part de lexpression de cest dire n u 1 1 n n u nu u e et on compose avec le LN des deux cts de lgalit notons que daprs la question II3a on a 0 nu gt 1 1 1 1 1 1 ln ln ln ln ln n n n n n u u n n u u e u e u u k u On passe la somme terme terme 1 1 1 1 1 ln ln n n n k k k k k u u 1 2 3 0 1 2 1 1 ln ln ln ln ln ln ln ln n n n k u u u u u u u u u k 1 Aprs simplification il reste 0 1 1 ln ln n n k k u u u Comme alors de plus 0u 1 0 lnu 0 1 1 0 1 2 1 1 0 n n k n k k u u u u u u k n v dcalage dindice Alors 1 ln ln n n n v u u tant strictement positif nu b Limite de vn Nous savons daprs la question II3a que lim n n u do 1 lim 0 n n u Comme 1 ln n n v u alors 1 lim lim ln n n n n v u La suite est divergente et nv lim n n v 14

III Etude de F F est la fonction dfinie sur lintervalle 0 par 2 2 4 0 2ln2 x x F x f t dt x F gt 1 Un encadrement a Valeur dune intgrale On a 2 2 2 2 4 4 2 2 2 2 2 ln ln 4 ln ln 4 ln ln ln4 ln 2 2ln2 x x x x dt t x x x x t b Encadrement de e- t 1 gtgt 1 t e t A la question II1 on a montr que pour tout rel x on a 1 x e x Posons x t lingalit devient alors 1 autrement dit t e t 1 t e t gtgt 1 0 t e On a 0 0 1 1 t t t t e e gt lt lt lt 0 Finalement pour tout rel t strictement positif on a 1 0 t t e 2 Continuit et drivabilit de F droite de zro a Encadrement de Fx 2ln2 Il sagit de montrer que pour tout rel x strictement positif on a 2 3 x F x 2ln2 0 pour cela on utilise lencadrement tablit la question prcdente gtt 0 on a 1 0 t t e On divise ensuite les membres de cette ingalit par t t est strictement positif ce qui donne 1 1 0 t e t t On intgre ensuite cette ingalit sur lintervalle 2 2 x 4x il vient 2 2 2 2 2 2 4 4 4 x x t x x x x e d dt dt t t t autrement dit 2 2 2 2 4 4 x x x x dt dt F x t On a vu la question III1a que 2 2 4 2ln2 x x dt t de plus do 2 2 4 2 3 x x dt x 2 3 x F x 2ln2 0 15

Finalement 2 3 x F x 2ln2 0 b Continuit et drivabilit de F droite de zro gtgt Continuit de F droite de zro Il sagit de montrer que lim 0 x F x F pour cela on utilise lencadrement de la question prcdente On a 2 lt 3 x F x 2ln2 0 On passe la limite notons que le passage la limite fait passer les ingalits strictes en ingalits larges 2 0 0 lim 3 lim 2ln2 0 x x x F x Comme alors daprs les thorme des gendarmes on a do 2 lim 3 0 x x lim 2ln2 0 x F x lim 2ln2 0 x F x F F est donc continue droite de zro gtgt Drivabilit de F droite de zro On part galement de lencadrement 2 3 x F lt x 2ln2 0 et on fait apparatre le taux daccroissement de F droite de zro gtx 0 on a 0 0 2ln2 0 0 3 0 3 0 lim 3 lim 0 0 x x F x F x F F x F x x x x x x lt lt 0 Comme et lim 3 0 x x 0 lim 0 x 0 F x F F x alors daprs les gendarmes F est drivable droite de zro et F 0 0 3 Limite de F au voisinage de linfini a Majoration de t Pour tout rel t 1 f t est majore par t e 1 1 1 t e t t t t e e notons que lexponentielle est positive donc lingalit ne change pas de sens - Finalement 1 t t f t 16

b Limite de au voisinage de linfini Nous venons de montrer que pour tout rel t 1 on a t f t e lt de plus 0 t e f t t gt on en dduit alors que 0 t f t e lt lt On intgre ensuite cette ingalit sur lintervalle 2 2 x 4x il vient 2 2 2 2 2 4 4 4 0 0 x x x t t x x x 2 f t dt e dt F x e dt lt lt lt lt Par ailleurs do 2 2 2 2 2 2 4 4 4 x t t x x x x e dt e e e x 2 2 4 0 x x F x e e lt lt On passe la limite 2 2 4 0 lim lim x x x x F x e e Comme alors daprs les gendarmes on a 2 2 4 lim 0 x x x e e lim 0 x F x 4 Variations de F a La drive de F On commence par justifier la drivabilit de F sur lintervalle 0 et on donnera ensuite lexpression de F x Daprs la question III2b on a F drivable droite de zro Notons H la primitive de la fonction t e f t t 6 sur lintervalle 0 sannulant en x 1 donc 1 x t e H x dt t Nous avons donc est drivable sur 2 F x H4x Hx 2 F 0 car compose de fonctions drivables H 2 x 6 4x et 2 x 6 x gtgt Conclusion F est drivable sur 0 et 2 2 2 2 2 2 4 4 4 2 2 2 2 2 8 2 4 x x x x x x e e e e e e F x x x x x x x x 17
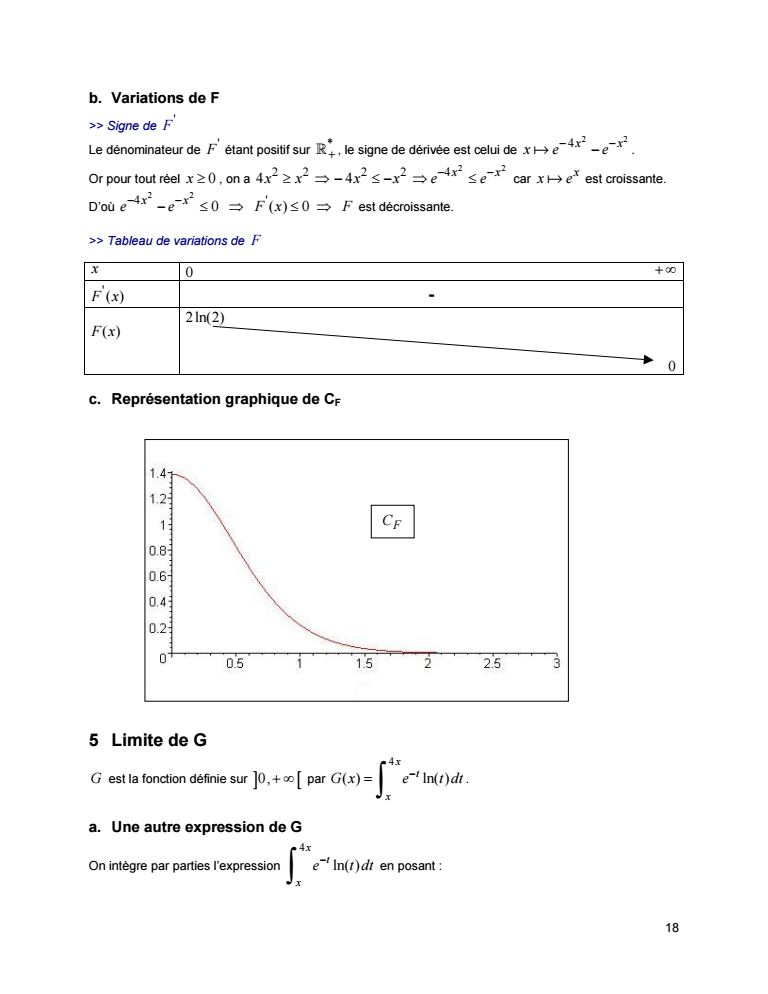
b Variations de F gtgt Signe de F Le dnominateur de tant positif sur F le signe de drive est celui de 2 2 4x x x e e 6 Or pour tout rel x 0 on a 2 2 2 2 2 2 4 4 4 x x x x x x e e car x x 6 e est croissante Do est dcroissante 2 2 4 0 0 x x e e F x F gtgt Tableau de variations de F x 0 F x - F x 2ln2 c Reprsentation graphique de CF CF 5 Limite de G G est la fonction dfinie sur 0 par G x 4 ln x t x e t dt dt a Une autre expression de G On intgre par parties lexpression en posant 4 ln x t x e t 18

1 ln t t u t t u t t v t e v t e Ce qui donne 4 4 4 ln ln4 ln x t x t x x x e G x t e dt x e x e F x t x pour tout x gt 0 Finalement pour tout rel x strictement positif on a bien 4 ln4 ln x x G x F x e x e x b Une limite Valeur de 4 lim ln x x x e e x Pour tout x strictement positif on a 4 4 ln ln x x x x e e e e x x x x On sait que et on calcule la valeur de lim ln 0 x x x 4 lim x x x e e x On pose 4 x x l x e e notons que l0 0 et que l est drivable donc 0 0 4 0 lim lim 0 x x 0 x x e e l x l l x x par ailleurs 4 x 4x l x e e do l 0 3 Finalement 0 0 4 4 lim ln lim ln 3 0 0 x x x x x x e e e e x x x x c Limite de Gx droite de zro On a montr la question III5a que pour tout x gt 0 on a 4 ln4 ln x x G x F x e x e x autrement dit 4 4 ln4 ln ln ln4 ln x x x 4 G x F x e x e x F x e x e e x x Soit 4 4 0 0 0 0 lim lim lim ln4 lim ln x x x x x x x G x F x e x e e On sait que 0 lim 0 2ln2 x F x F on sait galement daprs la question prcdente que 4 lim ln 0 x x x e e x Do lim 2ln2 ln4 2ln2 2ln2 0 x G x FIN 19

2004 4 10 ا ا ول ن و ي آ 10آات ء و 10آات اء ا quot amp ا آة ا إذا آquot اة ا - اء quotه إ ا وإذا آquot ء quot0 1 ا 3آات اء 34 quot آة ا 1 أ ا ل 8 ن ا8ن ا ن او 2 أ ا ل 8 ن ا8ن ا ن و 3 أ ا ل 8 ن ا8ن ا ن quot gt أ 4 ا ل 8 ن اة او ا - ء ن اة اltquot- ا - ء ا ا 3ط 3 2 1 E x y -دا 0 A ا م E FG H دا n 2 E -د A 14 3 21 4 n n وجا أن أ- 0 نأو 21 4 n و 14 3 n د ا أن L Mا ب- 21 4 n و 2 1 n د Fآا ك ampا 3MOا ه d 3 d 13 أو d 1 أن أ- d n 13 6 13 أن ب- 1quot n 2 R n FG ح H د Aآ AQأ 4 2 و A n n 21 17 4 3 2 B n n n 28 8 17 3 - Tا 0 n 1 -O S B و A دا أن أ- -ب n 3S ا3MO اamp ك اآF د A و B ا ا 4 ط ا ى اOي ب إ O u v 3V 3 a i ه يFTا هX م E O دا a ZO z O ا M طOا - T H 1 2 2 2 2 z z a a -أ د H -FG a i 1 - ا 0 H ampquot ب- أ 4 z a z a aa ZO z O ا M طOا - T C 2 C -FG أ- a i 1 - ا 0 C ampquot ب- أ -Vا - Tا 0 F quot 3 2 2 2 2 4 z z a a S z a z a aa u z a 1quotو 05 05 05 1 05 025 025 05 05 05 05 05 05 05 05

-Vا 0 8 S -Vا أن أ- 3 2 4 2 8 0 u u aa S u a u a a -ب quot1 i a re lt و r gt 0 R H و C 1 GO8 طOquot ق أ و r - د -ج اL M أن C 1GO8 و 4 Hث quotOط ه ؤ ر وس ltR وي اcع ا اا 10 ط و f - I و g اا اد ا0 ln 2 4 2 x f x xe و ln2 x g x x و C و ا اlt ا f و g ا ا 3 0 O i j 3V i j cm 4 ة ا أ -أf quot 1 و -ب د اgt اquot C 2 -أ أن ln 2 41 ln 2 x x IR f x x e -ب أط Qول g 8 ات اا- f -ج أن اد 2 1و ه ا ا ان د - f x 0 3 أدرس اا- g ا ت اgtوع اquot - g ا ات 3ا ltquot 0 و C ا 3Mر أ 4 e 27 ln 2 07 jkquot - ب h E فhquotا طOquot 8 1 14 ln 2 1 04 e R OO دا k - II 2 0 k e lt lt R و ل lt AFO8 g x k -دا أن quotF ZO 8 1أ- 1 2 lt lt -ب د S- اد R k ن ادان و ه اد- f x 0 F quot k اا- اد - 4 2 IR -0ا f kx k f x xe 41 أن آ8 أ- 2 kx k x IR f x kx e k ب - أط Qول g8ات f 3 k -أ اL M أن اد- 0 R b و a lt طF AFO8 f x 1 a b k lt lt -ب أ ن a و b أن اءQ - ل M 4أ - 2 0 1 1 t kx kt kt t IR xe dx kte e k A ا أ -ب k k I f x dx و - ln2 ln2 1 أن L Mا ج- R hS FQ lt OO د v و u نآ إذا هquotأ 5 ln ln u v u v ln ln 1 u v نn0 05 075 075 05 05 05 025 075 1 1 05 025 025 05 05 1 05 05 075 075

الشعبة علوم رياضية المدة 4 ساعات الامتحان الوطني الموحد لنيل شهادة البكالوريا دورة يونيو2003 المملكة المغربية وزارة التربية الوطنية و الشباب تمرين1 في نعتبر 2 التالية المعادلة 2 2 E xx yx 7 27 x y وليكن القاسم المشترك الأآبر للعددين x و 2 y ليكن y b و x a نضع 1- لنفترض أن x y حل للمعادلة E أن تحقق أ 2 22 a a bab 7 2 حيث k طبيعي صحيح عدد يوجد أنه استنتج ب 2 2 و a kb 7 2 2a b ka ت بين أن a 1 أن استنتج ث 2 2 b 1 8 2- حل في 2 E المعادلة تمرين2 G G المستوى منسوب إلى معلم متعامد ممنظم Oi j 3 2 16 نعتبر المنحنى E الذي معادلته 4 y x 1- أ بين أن E جزء من اهليج يتم تحديده ب أرسم المنحنى E نقطتين B03 و A 40 لتكن -2 النقطة نعتبر E من M1 أفصولها التي 1 حيث x 1 x 04 نضع حيث x1 1 4cost 1 0 2 t و نعتبر التكامل الآتي 1 4 2 1 3 16 4 x I x x dx أ باستعمال مكاملة بتغيير المتغير و ذلك بوضع x 4cost حيث 0 2 t بين أن 11 1 I xt t 6 3sin 2 03pts 050 050 050 075 075 3pts 050 050 125

ب لتكن S x 1 مساحة السطح المحصور بين المستقيمين OA و OM1 والمنحنى E ولتكن S مساحة السطح المحصور بين المستقيمين OA و OB والمنحنى E 3sin 1 t هو M1 تحقق أن أرتوب النقطة أحسب 1 بدلالة S x 1 t استنتج قيمة S أن بين -3 1 1 1 2 4 Sx S t إحداثيتي حدد M1 O OA OB النعلم في JJJG JJJG حالة في 1 4 t تمرين 3 من a b لكل -I 2 نعتبر المصفوفة a b ab b M b a M2 2لتكن E مجموعة المصفوفات الاتية في E M ab a b M حلقة تبادلية واحدية 2 نذآر أن 1- بين أن E جزء مستقر من M2 و من M2 2- بين أن E حلقة تبادلية واحدية 3 2 2- أ بين أن لكل عددين حقيقيين x و y لدينا x xy y x y 0 0 ب حدد العناصر التي تقبل مقلوبا في الحلقة E ج استنتج أن E جسم تبادلي II- ليكن عددا عقديا لا ينتمي الى 1- بين أن 1 أساس للفضاء المتجهي الحقيقي 2- نعتبر التطبيق من E نحو المعرف بما يلي a b E M a b بين أن تشاآل تقابلي من E نحو المعادلة في نعتبر -3 2 z z 1 0 حل في هذه المعادلة و أآتب حليها على الشكل المثلثي 025 025 025 025 025 45pts 075 025 050 025 050 025 075 075

4 1 3- نفترض في هذا السؤال أن 2 2 i بين أن تشاآل من E نحو تمرين4 I 2- لتكن f الدالة العددية المعرفة 0 بما يلي ln 1 4 2 x f x و ليكن C منحنى الدالة x Oi j ممنظم متعامد معلم في f G G i j cm 2 حدته و G G 1- أحسب lim x f x lim و x f x ثم حدد الفرعين اللانهائيين للمنحنى C 2 3- أ بين أن 1 2ln 0 4 x x fx x ب أعط جدول تغيرات f 3- بين أن المعادلة f x 0 تقبل بالضبط حلين مختلفين و بحيث 1 ln3 11 نعطي 1 3 e 4- حدد معادلة المماس T للمنحنى C في النقطة التي أفصولها 1 5- أرسم المنحنى C f المعرفة على 0 بما يلي III n- لكل عدد صحيح n بحيث n 4 نعتبر الدالة 2 ln 1 2 n x fx n x f في معلم متعامد ممنظم n المنحنى الممثل لدالة Cn و ليكن 1 n f- أدرس تغيرات الدالة و بين أنه يقبل نقطة انعطاف أفصولها 2 Cn- أدرس تقعر 5 6 e قارن أ -3 n و f x n 1 f x x قبم حسب Cn1 و Cn ب استنج الوضع النسبي للمنحنيين 0 المعادلة أن بين -4 n 1 u ev n n بحيث vn و un مختلفين حلين بالضبط تقبل f x متتالية تناقصية قطعا يمكن استعمال نتيجة السؤال 5 n n 4 u 3-III- بين أن 6- أ باستعمال نتيجة السؤال 2-II بين أن 1 3 4 ln 1 2 n n n n u u n uu 050 9pts 050 025 075 075 050 075 050 050 025 025 050 050 025

ب استنتج أن 2 2 4 1 2 3 n n n n u u n u n nu 1 4 1 ج بين أن 2 n e n u n n متقاربة محددا نهايتها n n 4 u د استنتج أن 7- أ بين أن 5 6 n ev 4 n نعطي 5 6 e 53 lim أن استنتج ب n n v 0 25 025 050 050 050

Corrig e Exercice 1 1 a On remplace x da et y db dans E d 2 a 2 d 2 a 2 7 db2da db d 2 a 2 d 2 a 2 7 d 2 b2a b a 2 d 2 a 2 7 b2a b b Dapres a ba 2 d 2 a 27 Or comme xy d ab 1 dou a 2 b 1 Par le th eoreme de Gauss b divise donc d 2 a 2 7 Par cons equent il existe k N tel que d 2 a 2 7 kb En rempla cant dans l egalit e du a il vient a 2 kb b2a b et comme b 6 0 a 2 k 2a b c a 2 k 2a b b aka 2 ab a a b a 1

d On a alors E d 2 7 b2 b E b 2 2b d 2 7 E b 2 2b 1 d 2 8 E b 12 d 2 8 2 Dapres 1 si x y est solution de E alors x x y cest-a-dire xy dou y bx et alors b 12 x 2 8 b 12 x 2 8 b 1 xb 1 x 8 23 Or b 1 x gt b 1 x et b 1 x b 1 x 2b 1 qui est paire donc b 1 x et b 1 x sont de meme parit e soit pairs comme leur produit est pair On a alors b 1 x 4 et b 1 x 2 qui sont les seules solutions On trouve alors le systeme suivant b 1 x 4 b 1 x 2 b x 3 b x 1 b 2 x 1 Or y bx 2 R eciproquement 1 2 est solution de E Donc S 1 2 Exercice 2 1 a E y 2 9 16 16 x 2 16y 2 9 x 2 16 x 2 4 2 y 2 3 2 1 On retrouve l equation dune ellipse centr ee en O daxe Ox de demi-grand axe a 4 et de demi-petit axe b 3 E est la partie de cette ellipse situ ee au-dessus de laxe Ox
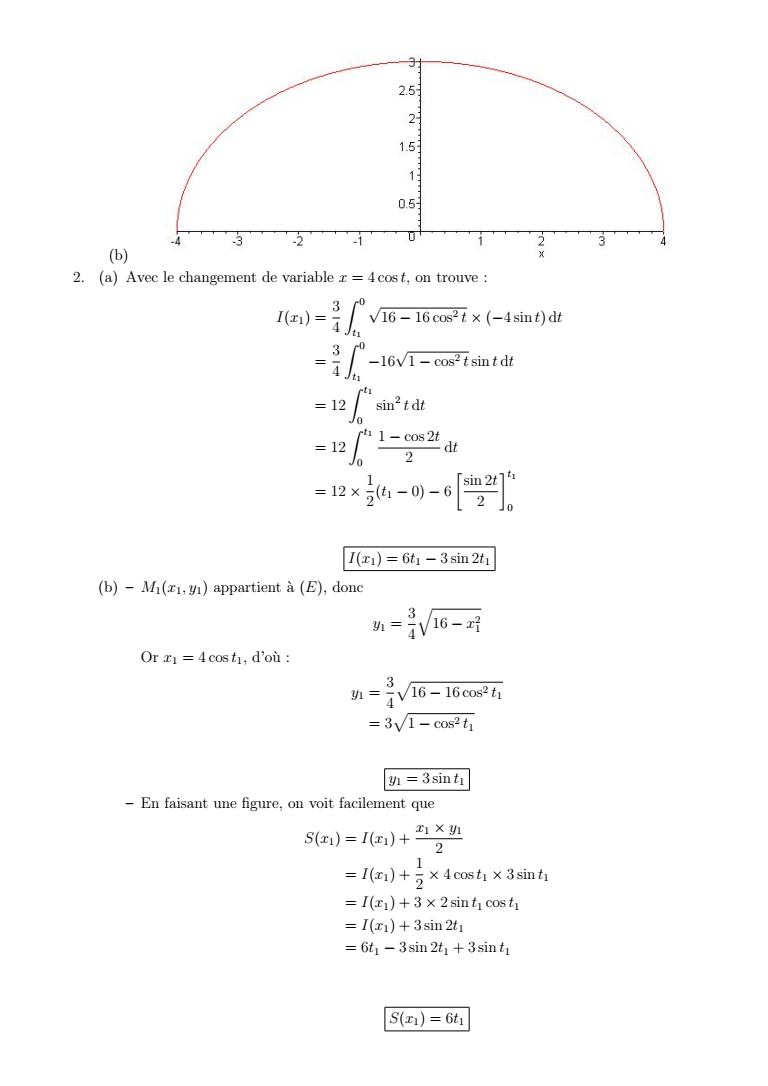
b 2 a Avec le changement de variable x 4 cost on trouve Ix1 3 4 Z 0 t1 16 16 cos2 t 4 sin t dt 3 4 Z 0 t1 16 1 cos2 tsin t dt 12 Z t1 sin2 t dt 12 Z t1 1 cos 2t 2 dt 12 1 2 t1 0 6 sin 2t 2 t1 Ix1 6t1 3 sin 2t1 b M1x1 y1 appartient a E donc y1 3 4 q 16 x 2 1 Or x1 4 cost1 dou y1 3 4 p 16 16 cos2 t1 3p 1 cos2 t1 y1 3 sin t1 En faisant une figure on voit facilement que Sx1 Ix1 x1 y1 2 Ix1 1 2 4 cost1 3 sin t1 Ix1 3 2 sin t1 cost1 Ix1 3 sin 2t1 6t1 3 sin 2t1 3 sin t1 Sx1 6t1

Clairement S S0 S4 cos 2 6 2 3 On a l equation Sx1 1 2 S 6t1 3 2 t1 4 M1 a pour coordonn ees 4 cost1 3 sin t1 donc OM1 4 cost1 3 sin t1 cost1 4 sin t1 3 cost1 OA sin t1 OB Dou pour t1 4 M1 a pour coordonn ees M1 2 2 2 2 Exercice 3 I 1 Soit Ma1b1 Ma2b2 E Ma1b1 a1 b1 b1 b1 a1 Ma2b2 a2 b2 b2 b2 a2 Pour la somme Ma1b1 Ma2b2 a1 a2 b1 b2 b1 b2 b1 b2 a1 a2 Ma1a2b1b2 E Donc E est stable pour la loi Pour le produit Ma1b1Ma2b2 a1 b1a2 b2 b1b2 a1 b1bb1a2 b1a2 b2 a1b2 b1b2 a1a2 a1a2 a1b2 b1a2 b1b2 b1b2 a1b2 b1b2 b1a2 b1a2 b1b2 a1b2 b1b2 a1a2 a1a2 b1b2 a1b2 b1b2 b1a2 a1b2 b1b2 b1a2 a1b2 b1b2 b1a2 a1a2 b1b2 Ma1b1Ma2b2 Ma1a2b1b2a1b2b1b2b1a2 E Donc E est stable pour la loi E est donc une partie stable de M2R et de M2R

2 E est un sous-groupe de M2R car E est non vide et E est stable par et pour tout Mab E on a Mab Mab E En outre la stabilit e de E par suffit pour conclure que E est un sous-anneau de lanneau M2R Pour tout a1 b1 et a2 b2 de R 2 on a Ma2b2Ma1b1 a2 b2a1 b1 b1b2 a2 b2b1 b2a1 a1 b1b2 a2b1 b1b2 a1a1 a1a2 b1b2 a1b2 b1b2 b1a2 a1b2 b1b2 b1a2 a1b2 b1b2 b1a2 a1a2 b1b2 Ma1a2b1b2a1b2b1b2b1a2 Ma2b2Ma1b1 Ma1b1Ma2b2 Donc E est un anneau commutatif Puisque I M10 E E est unitaire et dunit e la matrice unit e I 3 a R esolvons l equation du second degr e x 2xyy 2 0 en x L equation a pour discriminant y 2 4y 2 3y 2 6 0 L equation admet une solution r eelle uniquement pour y 0 Cette solution est alors x y 2 Ainsi x 2 xy y 2 0 x y 0 b Un el ement Mab de E est inversible si et seulement si detMab 6 0 Or detMab aa b b 2 a 2 ab b 2 Le d eterminant est donc nul uniquement si a b 0 soit pour M00 Ainsi tous les el ements de E sauf M00 sont inversibles c E est un anneau commutatif non r eduit a 0 et tout el ement non nul de E est inversible pour le produit Par cons equent E est un corps commutatif II 1 Posons u x iy avec x R et y R u nest pas r eel Soit a b R 2 montrons que a ub 0 a b 0 a ub 0 a xb iyb 0 a xb 0 yb 0 Or y 6 0 donc on a b 0 ce qui donne aussi a 0 Ainsi a b R 2 a ub 0 a b 0 Donc 1 u est une famille libre Montrons que 1 u est g en eratrice Prenons alors v C et montrons quil existe a b R 2 tels que v a bu On a v v1 iv2 avec v1 v2 R 2 et a b R 2 a bu a xb iyb

Soit en posant b v2 y et a v1 bx v1 v2x y on a bien a b R 2 tels que a bu v1 v2x y v2 y x i v2 y y v1 iv2 v Par cons equent v C a b R 2 v a bu Donc 1 u est une famille g en eratrice Par cons equent 1 u est une base de lespace vectoriel r eel C 2 Soit Ma1b1 Ma2b2 E 2 Alors Ma1b1 Ma2b2 Ma1a2b1b2 a1 a2 b1 b2u a1 b1u a2 b2u Ma1b1 Ma2b2 Ma1b1 Ma2b2 est donc un morphisme de E dans C Montrons que est bijective On voit clairement qua chaque matrice Mab E correspond un unique couple a b R 2 et r eciproquement De plus comme 1 u est une base de C a chaque z C correspond un unique couple a b R 2 tel que z a bu et r eciproquement Par cons equent a chaque matrice Mab E correspond un unique z C et r eciproquement donc est bijective On a donc montr e que est un isomorphisme de groupe de E sur C 3 L equation dans C z 2 z 1 0 a pour discriminant 1 4 3 Elle admet donc deux solutions complexes conjugu ees a savoir z 1 i 3 2 Donc S 1 i 3 2 1 i 3 2 Sous forme trigonom etrique cela nous donne S n cos 3 isin 3 cos 3 isin 3 o 4 Remarquons premierement que u est solution de l equation z 2 z 1 0 donc u 2 u 1 On a Ma1b1 Ma2b2 Ma1a2b1b2a1b2b1b2b1a2 a1a2 b1b2 a1b2 b1b2 b1a2u et Ma1b1 Ma2b2 a1 b1ua2 b2u a1a2 a1b2 b1a2u b1b2u 2 a1a2 a1b2 b1a2u b1b2u 1 a1a2 b1b2 a1b2 b1b2 b1a2u

Ma1b1 Ma2b2 Ma1b1 Ma2b2 Dou est un morphisme de E vers C On a montr e auparavant que est bijective donc est un isomorphisme de E sur C Exercice 4 I 1 En 0 lim x0 ln x et lim x0 4 x 2 dou lim x0 fx En lim x ln x x 2 donc lim x fx 1 2 Donc C admet une asymptote horizontale en d equation y 1 2 2 a f est d erivable sur 0 comme quotient et somme de fonctions d erivables sur cet intervalle Pour tout x de 0 f x 4x 2x 2x ln x x 4 f x 41 2 ln x x 3 b Pour tout x gt 0 x 3 gt 0 donc f x est du signe de 1 2 ln x x 7 1 2 ln x est strictement d ecroissante car ln est strictement croissante sur 0 et sannule pour ln x 12 x e On a donc le tableau de variations suivant pour f x 0 e f 2e1 12 f amp 12 3 f est d erivable donc continue sur 0 f est continue et strictement croissante sur 0 e donc la restriction de f a 0 e est une bijection de 0 e sur 2e1 12 Ainsi tout el ement de 2e1 12 admet un unique ant ec edent par f dans 0 e Or 0 2e1 12 donc l equation fx 0 admet une unique solution a dans 0 e De meme f est continue et strictement d ecroissante sur e donc la restriction de f a e est une bijection de e sur 2e1 12 12 Ainsi tout el ement de 2e1
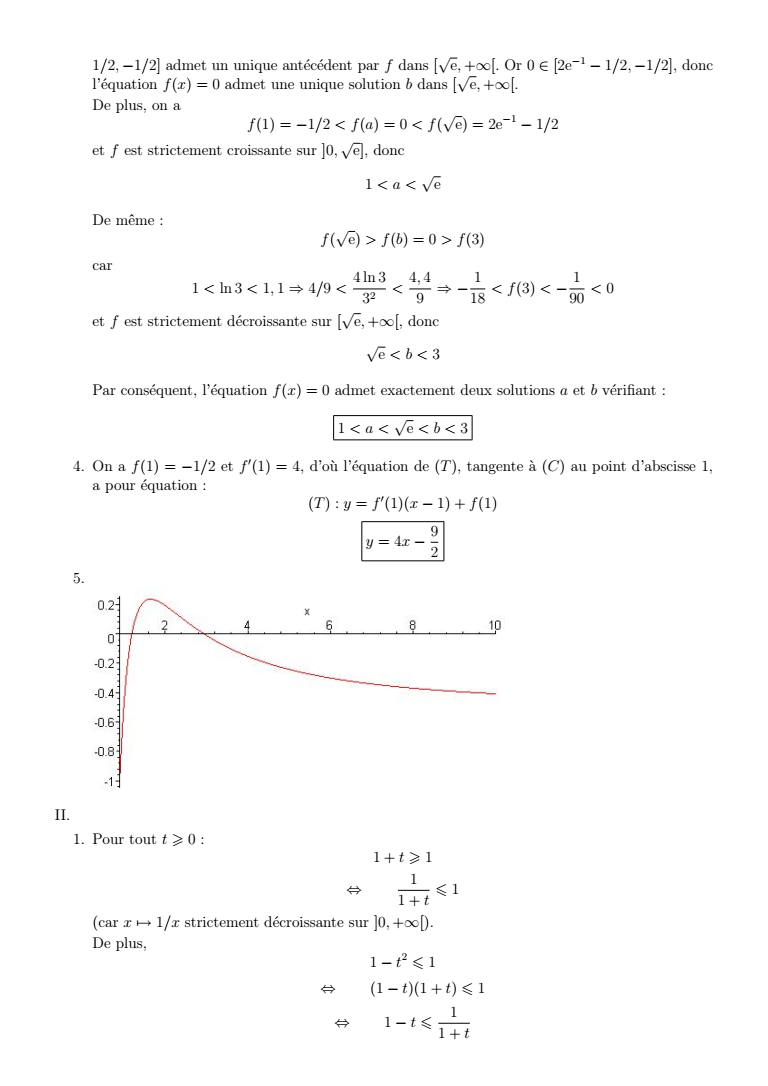
12 12 admet un unique ant ec edent par f dans e Or 0 2e1 12 12 donc l equation fx 0 admet une unique solution b dans e De plus on a f1 12 lt fa 0 lt f e 2e1 12 et f est strictement croissante sur 0 e donc 1 lt a lt e De meme f e gt fb 0 gt f3 car 1 lt ln 3 lt 1 1 49 lt 4 ln 3 3 2 lt 4 4 9 1 18 lt f3 lt 1 90 lt 0 et f est strictement d ecroissante sur e donc e lt b lt 3 Par cons equent l equation fx 0 admet exactement deux solutions a et b v erifiant 1 lt a lt e lt b lt 3 4 On a f1 12 et f 1 4 dou l equation de T tangente a C au point dabscisse 1 a pour equation T y f 1x 1 f1 y 4x 9 2 5 II 1 Pour tout t gt 0 1 t gt 1 1 1 t 6 1 car x 7 1x strictement d ecroissante sur 0 De plus 1 t 2 6 1 1 t1 t 6 1 1 t 6 1 1 t

car 1 t gt 0 Dou on trouve la double in egalit e cherch ee pour tout t de 0 1 t 6 1 1 t 6 1 2 En int egrant la relation pr ec edente entre 0 et a Z a 1 t dt 6 Z a dt 1 t 6 Z a dt a a 2 2 6 ln1 t 6 a III 1 fn est d erivable sur 0 comme quotient de fonctions d erivables Pour tout x de 0 f n x n 1 2 ln x x 3 Les variations sont les memes que pour f 2 f n est aussi d erivable sur R et pour tout x de R f 00 n x n 2x 3x 3x 2 1 2 ln x x 6 f 00 n x n 6 ln x 5 x 4 On a n gt 0 x 4 gt 0 donc f 00 n est du signe de x 7 6 ln x 5 qui est strictement croissante sur 0 et sannule pour x e56 Ainsi f 00 n est strictement n egative sur 0 e 56 sannule en e56 et est strictement positive sur e56 Dou Cn est concave sur 0 e 56 convexe sur e56 3 a fn1x fnx ln x x 2 et pour tout x de 0 x 2 gt 0 donc pour 0 lt x lt 1 fn1x lt fnx pour x gt 1 fn1x gt fnx En x 1 fn1x fnx 4 On prend exactement la meme d emonstration quau I-3 en rempla cant a et b par un et vn 5 On sait que pour tout x de 1 fn1x gt fnx Or un 1 dou fn1un gt fnun 0 Or fn1un1 0 dou fn1un gt fn1un1 fn1 est strictement croissante sur 1 e et un un1 1 e donc un gt un1 La suite unngt4 est donc strictement d ecroissante

6 a Pour tout n gt 4 un gt 1 donc un 1 gt 0 En appliquant la formule de II-2 on trouve alors un 1 un 12 2 6 ln un 6 un 1 un 12 un 1 2 6 ln un 6 un 1 un 13 un 2 6 ln un 6 un 1 b Partons du fait que fnun 0 fnun n ln un u 2 n 1 2 ln un u 2 n 2n Or dapres la question pr ec edente ln un u 2 n 2n 6 un 1 De plus un 13 un 2 6 ln un u 2 n 2n un 1 6 2u 2 n 2n3 un la division par 3 un ne change pas le sens de lin egalit e car un lt e lt 3 Ainsi on trouve lin egalit e cherch ee pour tout n gt 4 u 2 n 2n 6 un 1 6 u 2 n n3 un c Par ailleurs on sait que 1 lt un lt e donc 1 2n 6 u 2 n 2n et u 2 n n3 un 6 e n3 un De plus un 6 e 1 65 6 2 un 1 6 3 3 un gt 1 1 3 un 6 1 e n3 un 6 e n Ainsi on trouve 1 2n 6 un 1 6 e n

d Clairement lim n 1 2n lim n e n Donc dapres le th eoreme des gendarmes lim n un 1 0 dou lim n un 1 7 a Calculons fne56 pour tout n gt 4 fne56 5n 6e53 1 2 gt 5 4 6 5 3 1 2 gt 0 12 gt 0 Or fnvn 0 donc fne56 gt fnvn dou comme vn e 56 vn gt e 56 b Pour tout n gt 4 par d efinition fnvn 0 donne v 2 n 2n lnvn Le 7a donne ln vn gt 56 Dou v 2 n gt 5 3 n vn gt r 5 3 n Et comme lim n r 5 3 n on a lim n vn

الشعبة علوم رياضية المدة 4 ساعات الامتحان الوطني الموحد لنيل شهادة البكالوريا الدورةالاستدراآية يوليوز2003 المملكة المغربية وزارة التربية الوطنية و الشباب تمرين1 لدينا صندوقان U وV الصندوق U يحتوي على 4 آرات حمراء و 4 آرات زرقاء الصندوق V يحتوي على آرتين حمراويين و 4 آرات زرقاء نعتبر التجربة الاتية نسحب عشوائيا آرة من الصندوق U اذا آانت حمراء نضعها في الصندوق V ثم نسحب عشوائيا آرة من الصندوق V و اذا آانت زرقاء نضعها جانبا ثم نسحب عشوائيا آرة من الصندوق V ولتكن الأحداث التالية quot الكرة المسحوبة من U حمراءquot R1 quot الكرة المسحوبة من U زرقاءquot B1 quot الكرة المسحوبة من Vحمراءquot R2 B2 quot الكرة المسحوبة من Vحمراءquot 1- أحسب احتمال R1 و B1 B2 علما أن R1 محققquot و احتمال quotB2 علما أن B1 محققquot 2- أحسب احتمال quot 2 أن بين -3 13 21 p B p R 2 استنتج -4 تمرين2 p i 5cos 3 sin نضع 0 2 بحيث حقيقيا عددا ليكن التالية E المعادلة في نعتبر 2 E z pz 2 16 0 ان تحقق أ -1 2 2 p i 3cos 5 sin 16 ب حل في المعادلة E نرمز ب z1 و z2 لحلي المعادلة E حيث z z 1 2 M2 اللتين و M1 نعتبر النقطتين 2 G G- المستوى العقدي منسوب الى معلم متعامد ممنظم مباشر Ouv z 2 z و 1 لحقاهما على التوالي تتغير على دائرة C ينبغي تحديد معادلتها M1 أ بين أنه عندما يتغير في 02 فان النقطة M1 2 M منتصف P لتكن ب و لتكن مجموعة النقط P عندما يتغير في 02 03pts 1 1 050 050 450 050 050 050 050

بين أن اهليج بؤرتاه النقطتان F و F اللتين لحقاهما 4 و 4- 3 4 4 16-أ بين أنه لكل عددين عقديين a و b من 4 لدينا 4 4 b a ab b a 2 1 ب استنتج أن 2 1 4 4 4 4 z z z z أن بين ج 11 2 2 MFMF M FM F 2 JJJJJG JJJJJJG JJJJJG JJJJJJG 3 cos 5 sin 15 x y هي P النقطة في للمنحنى T المماس معادلة أن بين أ -4 M1 2 M ب بين أن المماس T عمودي على تمرين 3 من a b لكل -I 2 نعتبر المصفوفة 2 2 a b a b M b a M2 2 2 لتكن E مجموعة المصفوفات الاتية في 21 EM a b a b نضع -1 3 22 22 3 A تحقق أن AE 2- أ- بين أن E جزء مستقر في M2 و أن القانون تبادلي فيE ب- بين أن جميع عناصر E تقبل مقلوبا في E بالنسبة لقانون الترآيب الداخلي ج- بين أن E زمرة تبادلية نضع -3 0 1 0 0 1 A من n لكل و n n 1 A A A المجموعة نعتبر n G An أ تحقق أن G E ب لتكن H مجموعة مماثلات مصفوفات G بالنسبة للعملية في E H Bn حيث n بين أن 3 22 22 3 B ج بين أن G H زمرة جزئية من E 050 050 050 050 050 03 025 050 050 050 025 050 050

تمرين4 ليكن -I n nx الدالة العددية المعرفة بما يلي gn نعتبر و ليكن Cn منحنى الدالة n gx xe gn Oi j ممنظم متعامد معلم في G G 1- أ- أدرس تغيرات gn ب- بين أن gn تقبل قيمة دنيا عند عدد حقيقي un يتم تحديده بدلالة n lim أحسب أ -2 n x g x lim و n x g x ب حدد الفرعين اللانهائيين للمنحنى Cn g و C2 g2 المثلين 1 و 3 C1- أ أدرس الوضع النسبي للمنحنيين أنشئ ب C1 و C2 ln 2 07 2 i j cm نأخد G G 4 2- أ باستعمال مكاملة بالأجزاء أحسب بدلالة x التكامل x t I x te dt g2 على 0ln 2 قصور الدالة h2 ب لتكن حول محور الأفاصيل h2 أحسب حجم مجسم الدوران المولد من دوران التمثيل المبياني ل v gu n nn نضع -5 متقاربتان و حدد نهايتهما n n v و n n u بين أن المتتاليتين f nx المعرفة على بما يلي II nنعتبر الدالة n f x xe f G G في معلم متعامد ممنظم n Ouv المنحنى الممثل لدالة n و ليكن 1 n f- أدرس تغيرات الدالة f x تقبل حلا وحيدا 2 n n-استنتج أن المعادلة 0 3 1- أ بين أن 1 ln 2 2 e لهما نفس الإشارة x x و 1 1 ب بين أن 4 1- أ لتكن الدالة المعرفة على 2 يلي بما x 1 x e x e 1 بين أن تناقصية على 2 1 1 ب استنتج أن x 1 e x e 950 050 050 050 050 050 050 050 050 1 050 050 025 050 050 050

نضع -5 0 1 2 1 n طبيعي صحيح عدد لكل و n n e حيث a حقيقي عدد يوجد أنه بين أ n n 1 1 1 n a متقاربة وحدد نهايتها n ب بين أن المتتالية 0 50 050 httpmathkasicima sdfdsfd httpmathkas9ecc
Chaymae Ihams
أرسلت .
- الملفات : الملفات.
- المستوى : الثانية باكالوريا.
- المادة : الرياضيات.
كلمات مفتاحية :
الامتحانات الوطنية التصحيح 2003 الى 2009
الامتحانات الوطنية التصحيح 2003 الى 2009