قواعد دراسة الدالة العددية
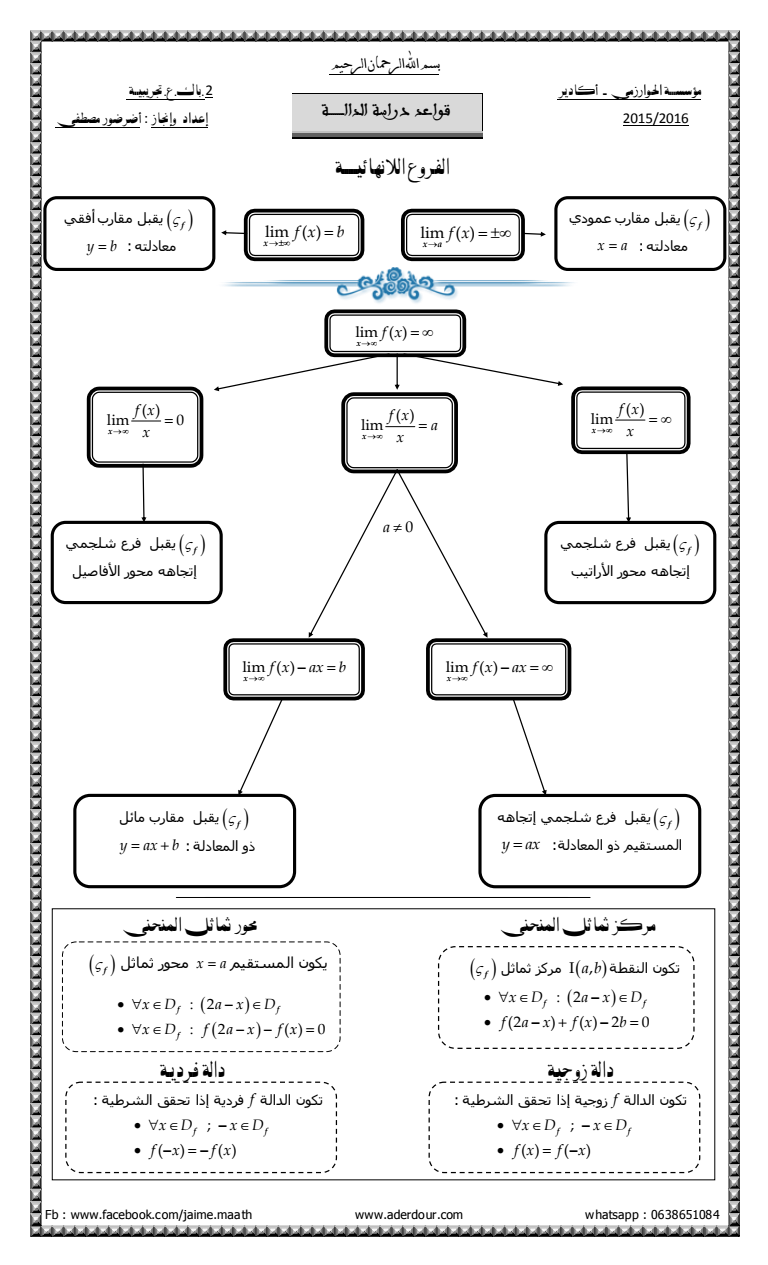
بسماهللالرمحانالرحيم Fb wwwfacebookcomjaimemaath wwwaderdourcom whatsapp 0638651084 مؤشصة احلوارزمي - أكادير 2باكعجتريبية 20162015 إعداد وإجناز أضرضور مصطفى الفروع الالنهائية a 0 قواعد دراسة الدااة مثم ممارب عمىدي f x a معادنره lim x a f x lim x f x b مثم ممارب أفم f y b معادنره lim x f x lim 0 x f x x lim x f x a x lim x f x x مثم فرع شهجم f إذجاهه محىر األراذة مثم فرع شهجم f إذجاهه محىر األفاصم lim x f x ax lim x f x ax b مثم فرع شهجم إذجاهه f y ax انمسرمم ذو انمعادنح مثم ممارب مائم f y ax b ذو انمعادنح مركس مثاثل املنحنى حمور مثاثل املنحنى ثماثم محىر x a كىن انمسرمم f 2 2 0 f f f x D a x D x D f a x f x دالة زوجية دالة فردية زوجح إذا ذحمك انشرطح f ذكىن اندانح f f x D x D f x f x فردح إذا ذحمك انشرطح f ذكىن اندانح f f x D x D f x f x ثماثم مركس I a b ذكىن انىمطح f 2 2 2 0 f f x D a x D f a x f x b

بسماهللالرمحانالرحيم Fb wwwfacebookcomjaimemaath wwwaderdourcom whatsapp 0638651084 املتطابقات اهلامة نقط تقاطع املنحنى مع احملورين املنحنى يقبل مقارب مائل األشلال الغري احملددة يف النهايات اإلشتقاق معادلة املناس الصلل القانوني lim x x f x f x x x لاتهح نإلشرماق ف f عى أن 0 x ومىه f مثم مماش معادنره 0 0 0 y f x x x f x 0 lim x x f x f x x x غر لاتهح نإلشرماق عهى سار أو مه f عى أن 0 x ومىه f مثم وصف مماش مىجه وحى األعهى أو األسفم عىد 0 0 A x f x 2 2 2 2 2 2 2 2 3 3 2 2 3 3 3 2 2 3 3 3 2 2 3 3 2 2 2 2 3 3 3 3 a b a ab b a b a ab b a b a b a b a b a a b ab b a b a a b ab b a b a b a ab b a b a b a ab b مكىك إسرعمال مثهث تاسكال نرحدد وشر اندرجح 4 و 5 نرحدد ومط ذماطع م f مع محىر األفاص f x 0 وحم انمعادنح نرحدد ومط ذماطع ة f مع محىر األرا f 0 وحسة ممارب مائم y ax b نىثه أن انمسرمم نهمىحىى f تجىار و وجدها جة أن وحسة انىهاح تجىار lim 0 مىعدمح x f x y أو 2 2 1 1 1 2 n n n n n f g f g f g f f g f g g g f f f f f f f f n f f n f f 1 3 2 2 1 2 1 3 1 1 n n a ax a x n x x x x x x x اندوال انمثهثح 2 2 1 tan 1 tan cos sin cos cos sin x x x x x x x مشرمح اندانح انعكسح 1 1 1 f x f f x مشرمح مركة دانره f g g x f g x عىد انىمطح ذاخ األفصىل ذكرة معادنح انمماش 0 x y f x x x f x 0 0 0 عهى شكم انشكم انماوىو نهحدودح 2 ax bx c هى 2 2 4 b a x a a I لاتهح نإلشرماق مرذه عهى f نركه كىن ب f x I f x 0 إذا كاود محد كىن f x I f x 0 إذاكاود ممعر وذغر اإلشارج ف f x 0 إذا كاود فإن x f مثم ومطح إوعطاف 0 0 A x f x I لاتهح نإلشرماق عهى انمجال f نركه x I f x 0 إذاكاود I ذسادح عهى f ذكىن x I f x 0 إذاكاود I ذىالصح عهى f ذكىن x I f x 0 إذاكاود I ثاترح عهى f ذكىن
Hatim Satri
ملخص شامل من إعداد أضرضور مصطفى
أرسلت .
- الملفات : الملفات.
- المستوى : الثانية باكالوريا.
- المادة : الرياضيات.
كلمات مفتاحية :
قواعد دراسة الدالة العددية
قواعد دراسة الدالة العددية